Derive the rotation matrix in a CUNNING WAY
Derive the rotation matrix in 30 seconds
![]()
Hmm… Annoying…
![]()
What’s wrong with you?
![]()
Ah, Mr. Penguin. I’d like to understand why the rotation matrix is expressed in the figure below but…
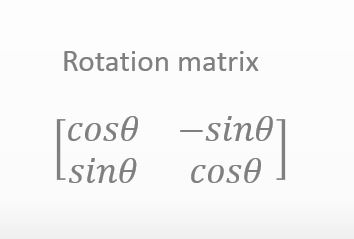
![]()
All website I’ve checked have so many calculations that I’m getting tired of it..
![]()
Rally? Actually, you can derive the rotation matrix in 30 seconds.
![]()
Seriously? Would you tell me the way?
![]()
Okay. Firstly, please tell me the coordinates of the two points in the figure below.
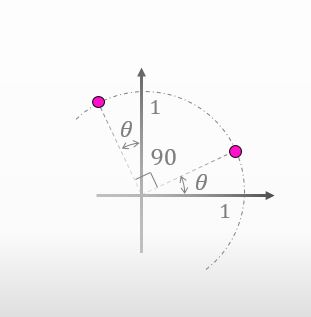
![]()
That’s easy. Here you are.
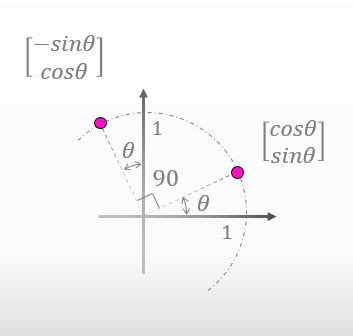
![]()
Good. Actually, there is another way to describe the points by using the rotation matrix R.
Please take a look at the figure below.
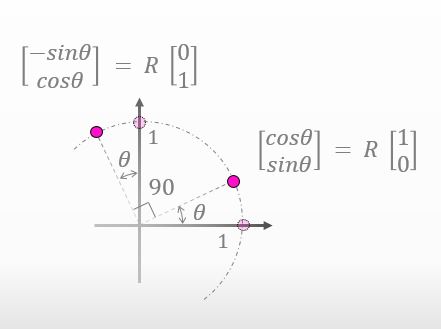
![]()
We haven’t known the values of the rotation matrix R are but yeah, if we can use the rotation matrix R, the points can be described like that.
![]()
We are going to go to the next step.
In the right side of the figure below, I made a point [x,y] rotate by Φ. You don’t have any questions regarding the rotated coordinate, right?
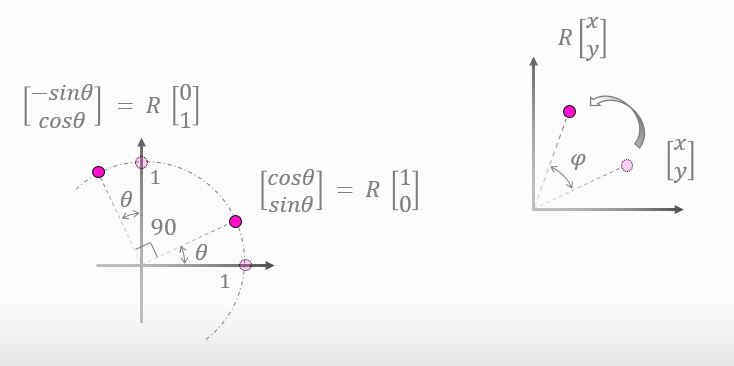
![]()
Yeah, that’s what the rotation matrix means. (I haven’t known the values of the rotation matrix R though…)
![]()
I added a equation in the right bottom side of the figure below. I just expanded the coordinate of the rotated point.
You don’t have any questions either, right?
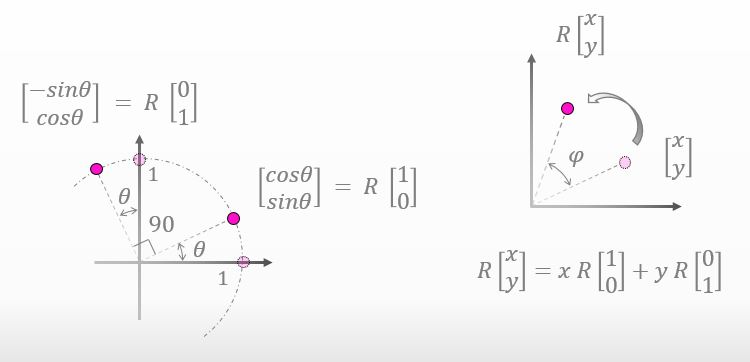
![]()
No questions. You just expanded R[x,y].
![]()
By the way, did you know that we’ve already known the values of R[1,0] and R[0,1]?
![]()
Eh… Ah, you are right. We’ve already got them.. The values are inside the red boxes.
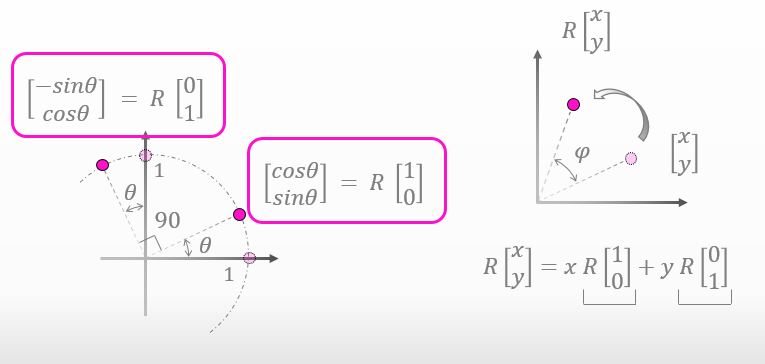
![]()
Will you substitute the values into the equation in the right bottom side in the figure above?
![]()
Sure.. Is this right?
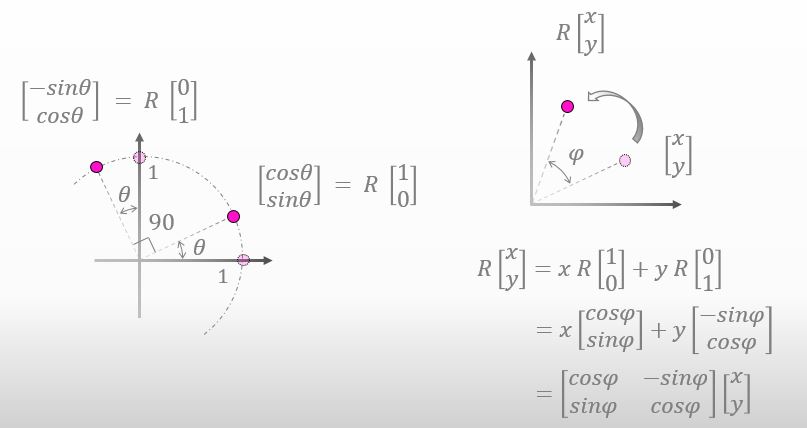
![]()
Did you realize something?
![]()
Well… Nope..
![]()
Really? Will you pay attention to the equation you derived more carefully?
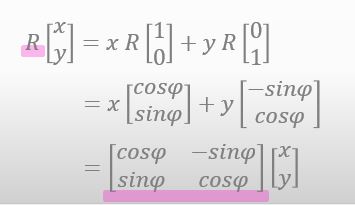
![]()
Ah, we’ve got the values of the rotation matrix…
![]()
Then, see you again.
![]()
Thank you so much.
