Get along with total differential and chain rule

 

 

 

 

 

 

 

Questions about total differential and chain rule

 

We are going to get along with “total differential” of two variables and “chain rule” today.

 

You are NOT going to prove them but help me get the clear picture of them, right? Sounds interesting.

 

Have you heard of total differential?

 

Yes, I’ve already studied them. I showed the expression of total differential of two variables below. I heard that it means the change in f(x) when both x and y change a little.

 

 

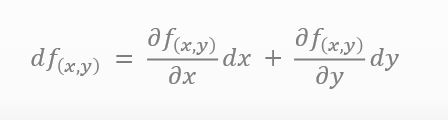
What is the reason?

 

In the class, our teacher showed the figure like below and told us that the figure explains total differential.

 

 

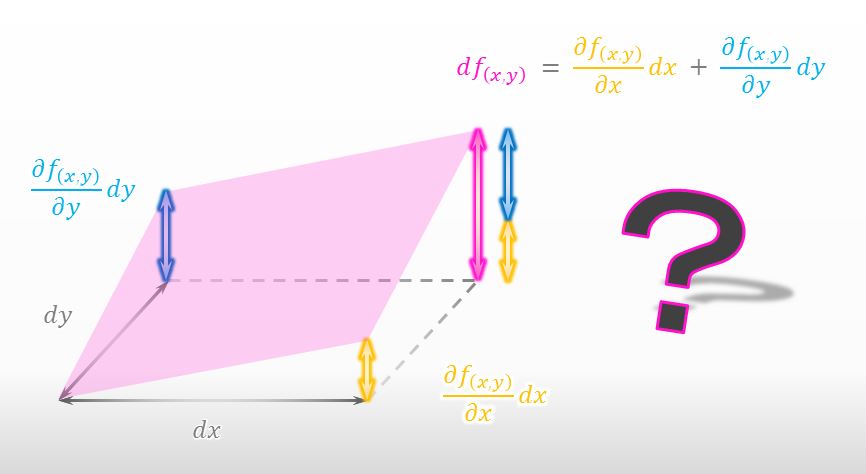
Have you got the clear idea of total differential with the explanation?

 

Well… Yeah, I felt like that’s the way it goes.

 

I see. Have you studied chain rule?

 

After I studied total differential, the teacher divided both sides of the equation of total differential by dt like below and then we were able to get chain rule.

 

 

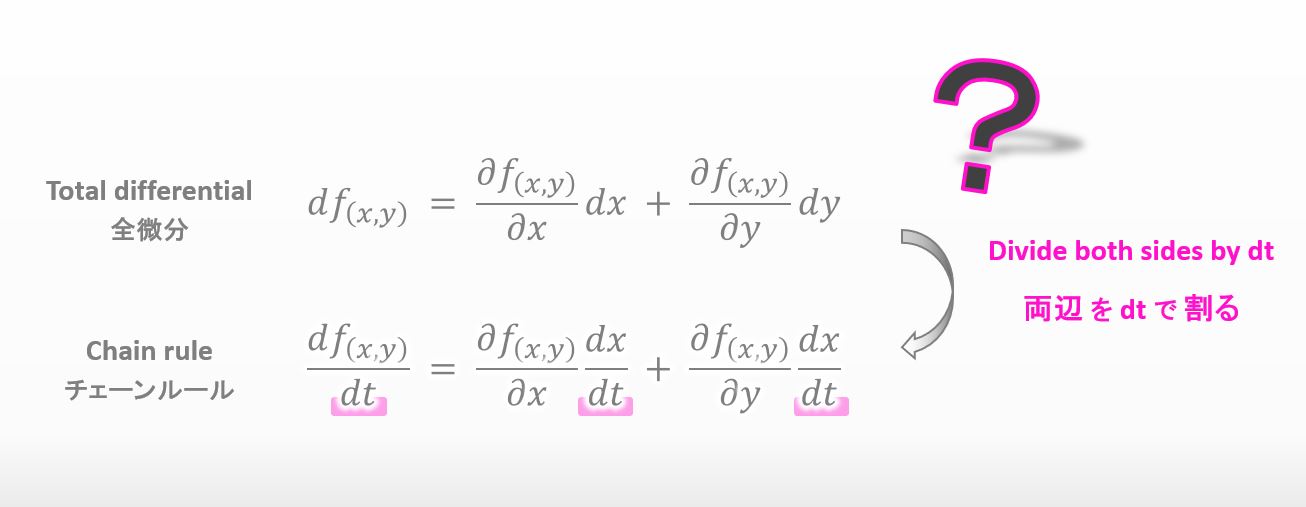
What if the parameter t is time, what do you think the chain rule means?

 

Well… I have no idea…

 

Then I’ll provide this lecture so that you can have visual understanding of chain rule.

 

Thank you. I’m looking forward to having this lecture.

 

I’ll start with total differential first.

 

 

Get the clear idea of total differential

 

Please take a look below. I prepared a 3D graph in the figure for this lecture.

 

 

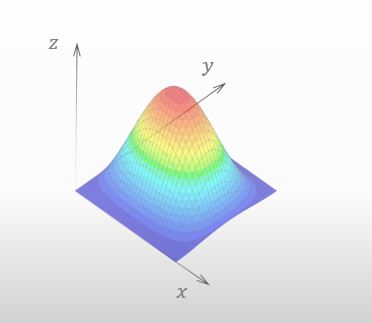
The shape is like a mountain.

 

Yes. I’d like you to pay attention to the small surface area on the mountain like below.

 

 

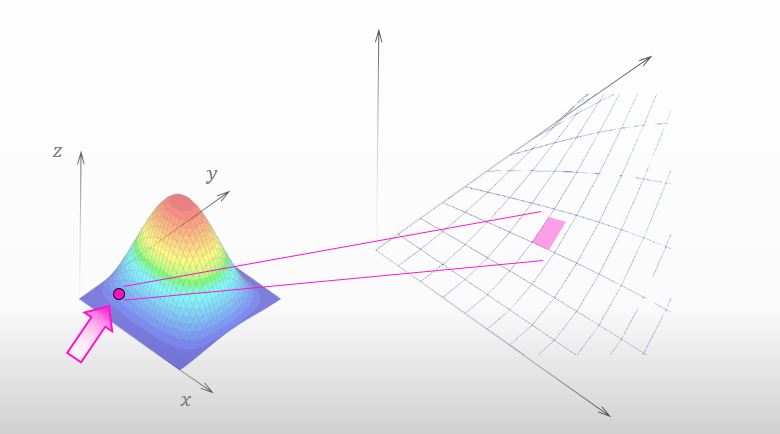
I studied in someone’s lecture about it before. The height of the red square is the meaning of total differential as shown below.

 

 

What kind of square is it?

 

If I’m not mistaken, it is a parallelogram…

 

We are going to check the small square one by one together.

Let’s say you are walking around the mountain and now you are at the point shown below.

 

 

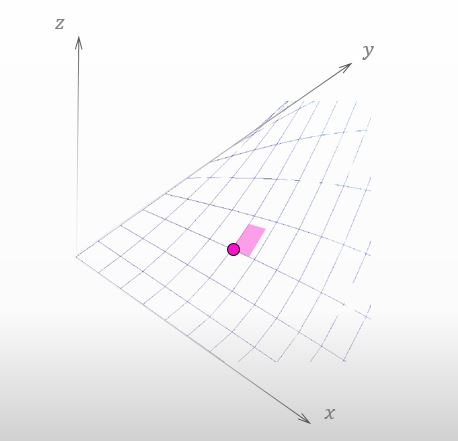
You moved a little with the value of y constant like the figure below. To put it more accurately, your “shadow” projected on the xy-plane moved toward the x-axis by dx.

 

 

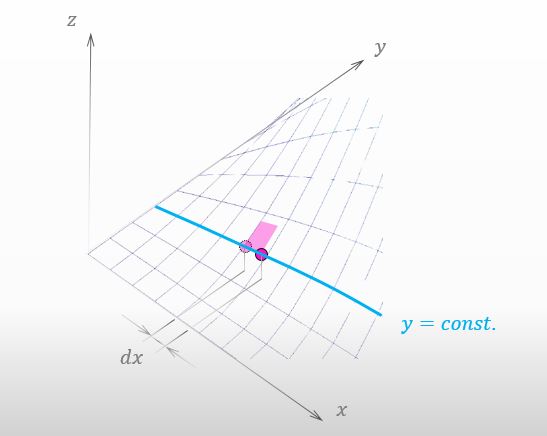
What is the blue line in the figure above?

 

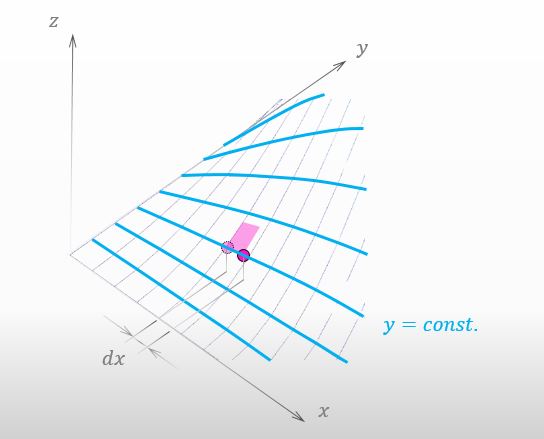
Sorry, I forgot to tell you about it. Please take a look at the figure below. There is no change in y on each of the blue curves.

 

 

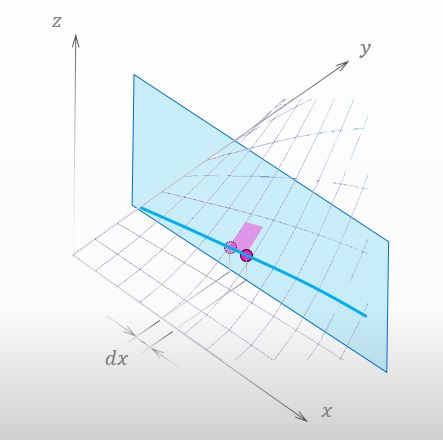
If I put an orthogonal plane to the y-axis in the mountain like the figure below, I can easily imagine that there is no change in y on the blue curve. The blue curve is the intersection between the mountain and the plane.

 

 

You gave me a good figure. We can easily understand that dx is not the length of the blue curve but the length of your shadow moved toward the x-axis.

 

I have a question. How much did I go up on the mountain while moving on the blue line?

 

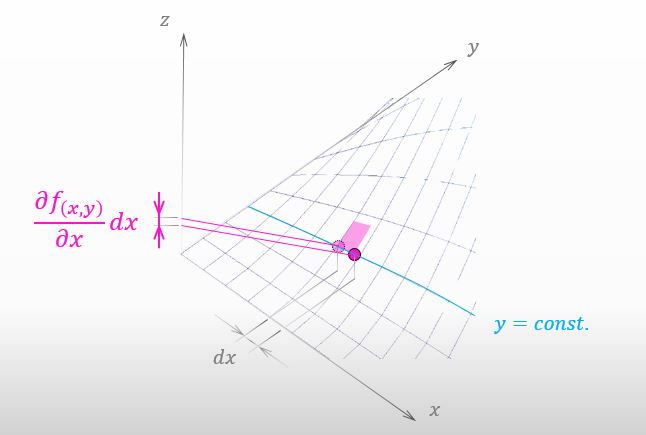
Please take a look at the figure below. It shows the amount of how much you went up.

 

 

I learned it in your lecture before. The lecture was not about 3D but 2D though. The title of the lecture was Get along with infinitesimal change and approximation

 

I’m glad that you remember it. The amount of climbing up on the mountain this time is the left term in the expression of total differential like the figure below.

 

 

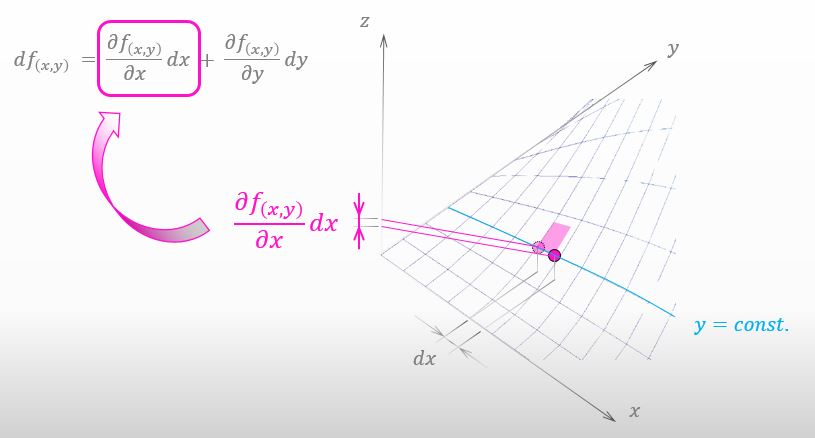
I understood what happens if my shadow moves toward the x-axis. I guess that the same thing will also happen regarding the y-axis. What I meant is if my shadow moves toward the y-axis by dy, the amount of how much I go up on the mountain is the right term of total differential like below.

 

 

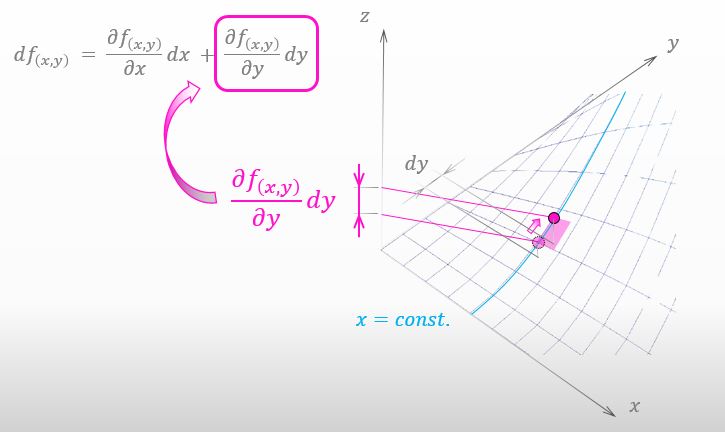
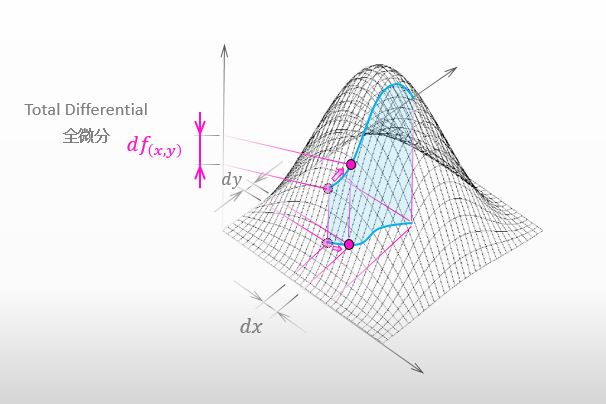
You are right. Actually, we are ready to understand the meaning of total differential. Please take a look at the figure below. I enlarged the small red surface we have been considering.

 

 

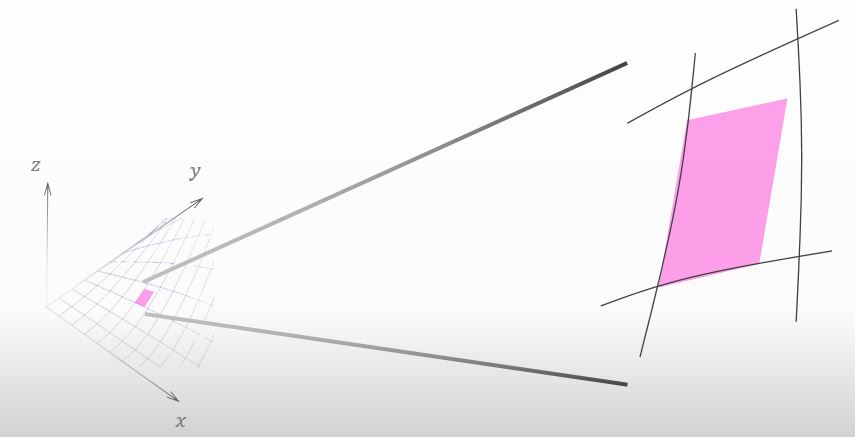
If I’m not mistaken, the shape of the red surface is a parallelogram.

 

Yes. The parallelogram is made by the three points like the figure below.

 

 

Yeah. A parallelogram is formed by three points.

 

Can you tell me what we have already known about the parallelogram?

 

We have already known how much I climbed up a while ago. I showed them below.

 

 

Thanks. Can you realize something?

 

Since we are considering a parallelogram, the total height of the parallelogram is equal to the value of total differential as seen below.

 

 

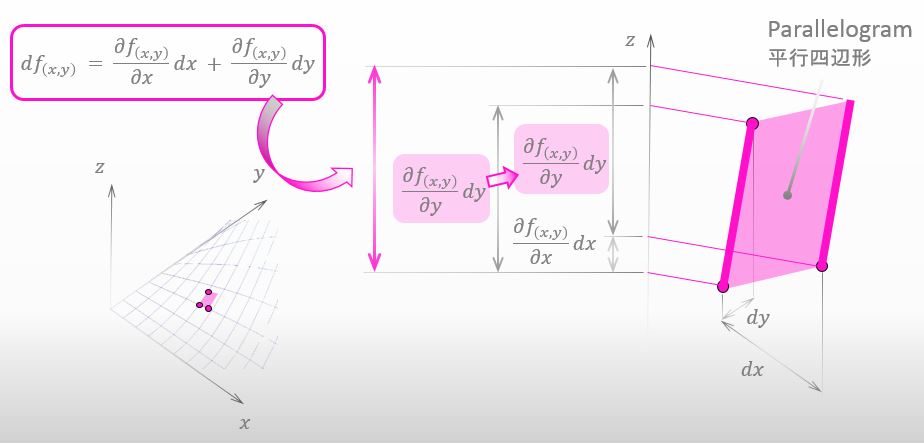
Great. You’ve got the clear idea of total differential.

 

 

Key point for helping to understand total differential

 

The key point for helping to understand total differential is that dx and dy are independent from each other.

 

What would you like to imply by that?

 

For example, you can apply the idea of total differential to both of the situations below. Both dx and dy can take any values freely. However, please keep in mind that the smaller a parallelogram is, the more accurate the approximation of total differential is.

 

 

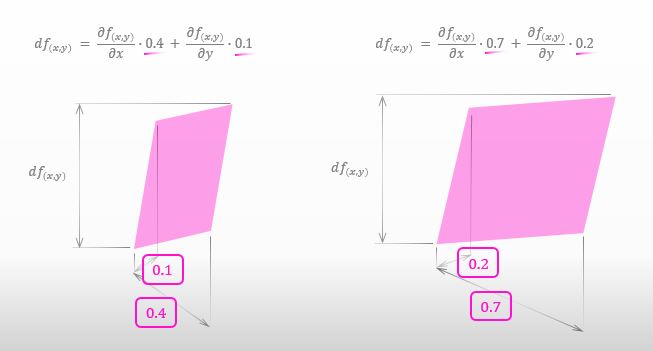
Why is it the key point of total differential to know that dx and dy are independent from each other?

 

It’s because that is different from chain rule.

 

 

Understand chain rule visually

 

Will you compare total differential and chain rule with each other?

 

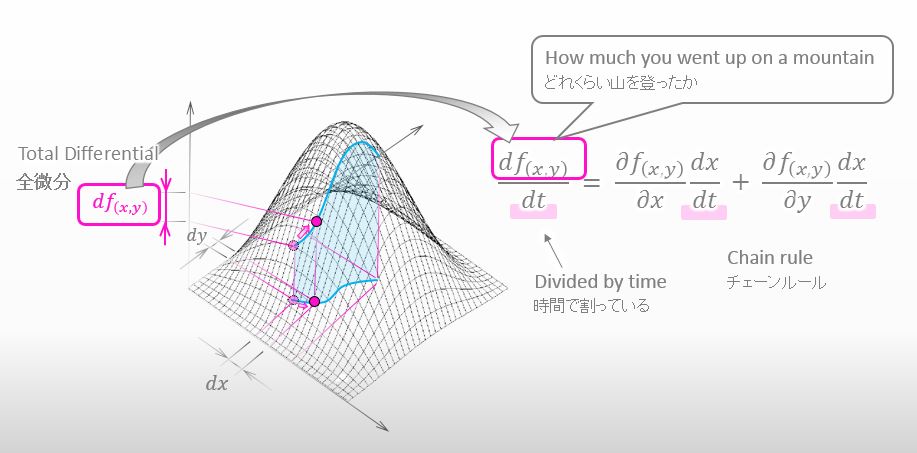
Please take a look below. The expression of chain rule includes total differential. The shape of the equation of chain rule looks derived by dividing both sides of total differential by dt.

 

 

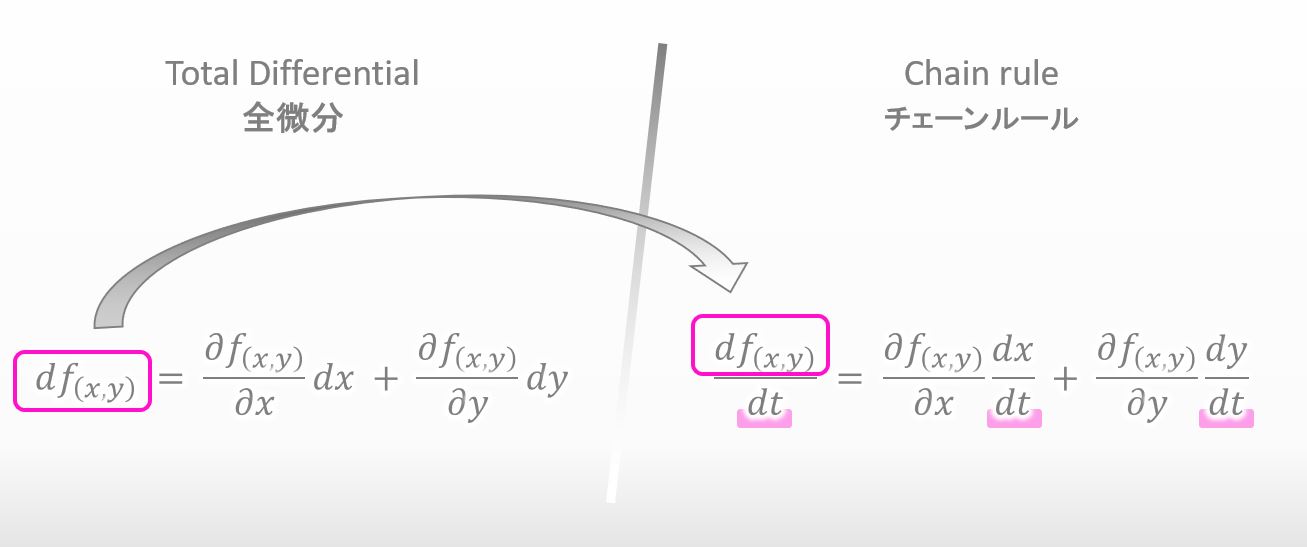
Yeah it looks like so. Do you still remember the meaning of total differential of two variables?

 

It means the amount of how much I go up on a mountain if my shadow projected on the xy-plane moves a little.

 

 

The shape of the equation of chain rule looks like the amount of how much you go up on a mountain derived by dt.

 

 

Chain rule expresses the rate of change of the amount of how much I go up with respect to “t”.

 

If you’d like to visually understand what the parameter “t” means, we need to keep in mind that dx and dy are related with each other in chain rule.

 

How are dx and dy related with each other?

 

The curve on the xy-plane below may enable you to understand the relation.

 

 

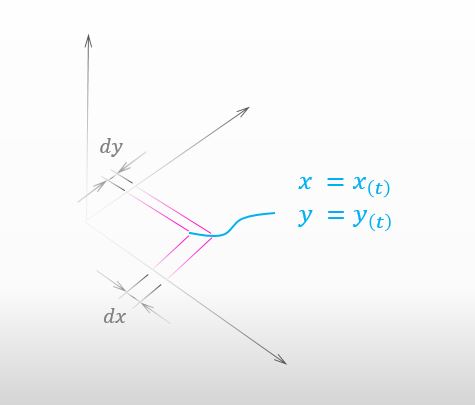
I see. I understood that dx and dy can’t take values freely because they have to move on the curve.

 

Right. Let’s say there is a little change in t as seen below.

 

 

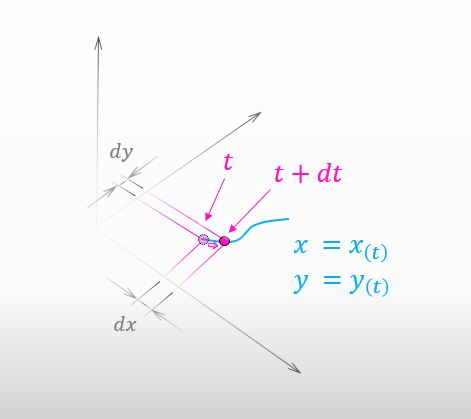
It means that my shadow moved a little on the blue curve. This time, the amount of how much I went up on the mountain is expressed like below.

 

 

Great. What do you think chain rule will mean if the parameter t is time?

 

If the parameter t is time, chain rule will divide the amount of how much I went up by time, and which means that chain rule is telling the amount of how much I go up on the mountain per unit time.

 

 

Perfect. Have you got the clear visual idea of chain rule?

 

Yes. Thank you so much.