三角関数と複素数の変換が可能なのはどんなとき?
三角関数と複素数の関係性
交流回路の授業の終わりにて
![]()
本日は、交流回路の計算をする際に複素数がとても有効であることを学びました。
交流回路の微分方程式を解く際には、以下の様に複素数を利用することが可能です。

あ、もう時間だ。では また来週。
三角関数はいつでも複素数に変換可能?
![]()
Hmm…
![]()
なんだか疑問が残っているみたいだね。
![]()
えぇ。実はそうなんです。フクロウ教授に騙されているような気がして。
![]()
なんでそう思うの?
![]()
もしも本当に交流回路の計算に複素数を使うことが出来たのだとしたら、電力の計算がとても簡単になるんですけど、その計算結果は間違ったものになってしまいますよね?
![]()
もう少し説明してくれる?
![]()
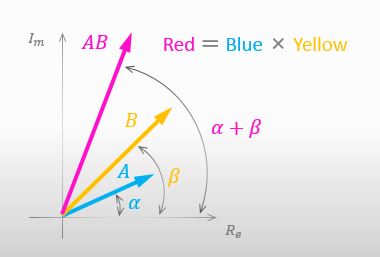
はい。まず最初に、複素数の掛け算の特長を以下に示しますね。
![]()
そうだね。もしも青い複素数と黄色い複素数の掛け算をするのなら、その結果(赤い複素数)の長さは両者の長さの積 つまり A×B になり、角度は両者の和 つまり α+β になるってことだね。
それで、どうやって複素数の積の特長を電力の計算に利用するつもりなの?
![]()
これが電力の計算式ですよね?
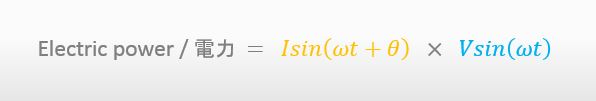
![]()
そうだよ。
![]()
もしも本当に複素数を利用できるのであれば、この計算はとても簡単になります。
以下にその計算を示してみますね。

![]()
ははは。それが間違っているってことは既にわかっているようだね。
![]()
そうなんです。それで困っているわけです。複素数を交流回路の計算に利用できる時もあれば、利用できない時もある。。。
以下の図を見てください。どちらも複素数の掛け算を利用しておりますが、左側の計算は完全に間違ってます。
どんなときに三角関数と複素数の変換が可能なのでしょうか?
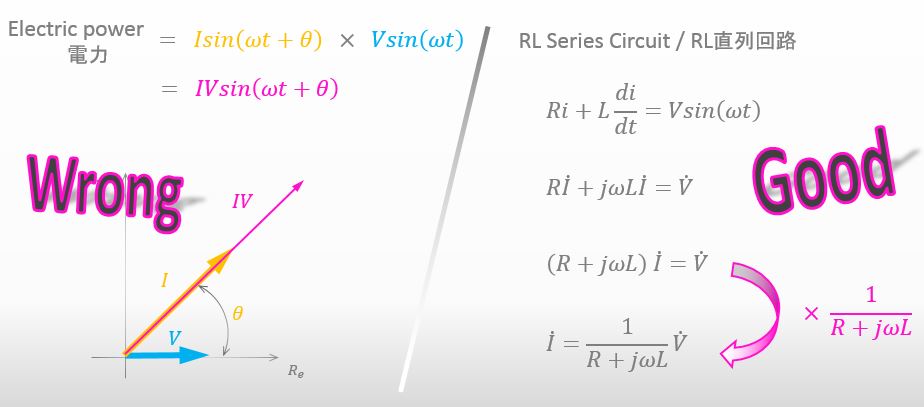
三角関数を複素数に変換可能な理由
![]()
君の疑問はわかったよ。ではまずは、何故交流回路において複素数を利用できるのか考えてみよう。
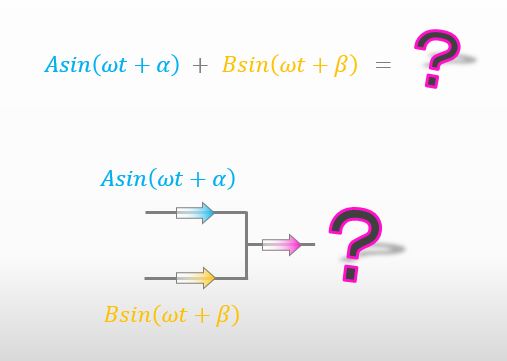
以下の足し算をすることって ある?
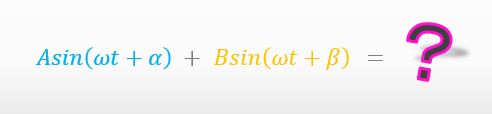
![]()
もちろんです。こんな風に2つの電流の足し算をするときですよね。
![]()
計算できる?
![]()
出来ると思います。複素数を使いばいいんですよね?フクロウ教授がおっしゃっていたように。
![]()
そうだね。じゃぁ複素数を使って実際に計算してみてちょうだい。
![]()
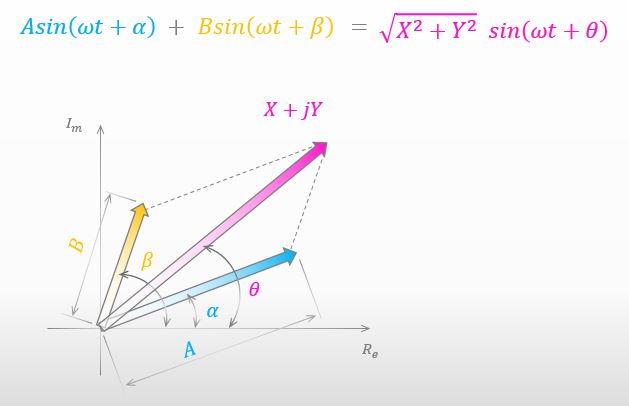
わかりました。こんな感じでどうでしょう?
![]()
いいね。でもなんでそういう計算ができるのか教えてくれる?
![]()
えぇっと… わかりません。フクロウ教授がおっしゃったように複素数を使っただけなので…
![]()
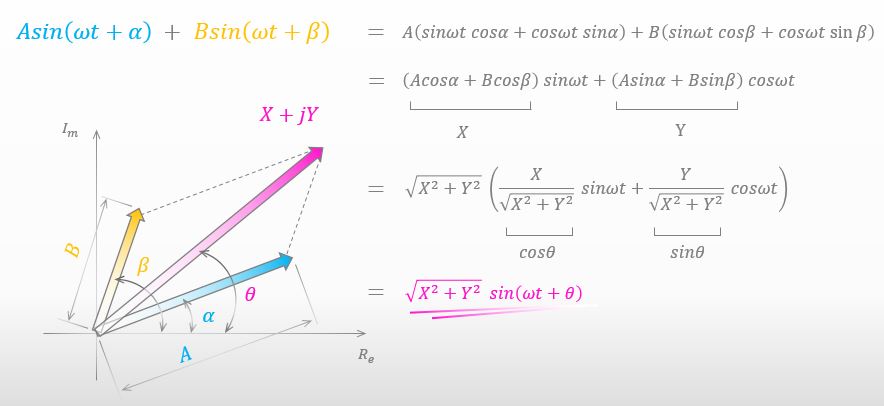
ははは。まぁいいでしょう。以下に、なぜ複素数を使えるのかっていう理由を示したから見てみて。ちなみに複素数は全く使ってないよ。
三角関数の足し算は、複素数の足し算みたいに振る舞う ってことは理解できたかな?
微分方程式に複素数を適用できる理由
![]()
なるほど。三角関数の足し算をするときには三角関数を複素数に変換できる理由はわかりました。でも、微分方程式を解くときにも複素数を利用できる理由は 依然謎のままです…
![]()
実は、微分方程式を解くときにいつも複素数を使えるわけじゃないんだよね。交流回路に関する微分方程式を解くときは、複素数は便利だけど。
![]()
え?もう少し説明していただけますか?
![]()
えぇよ。ちょいと以下の計算を見てみて。交流回路の微分方程式を解こうとしてるんだけどさ。

![]()
最後の計算で三角関数の和がでてきましたね。

![]()
良く気付いたね。三角関数の足し算をするときには、複素数が使えるってことは覚えているかな?

![]()
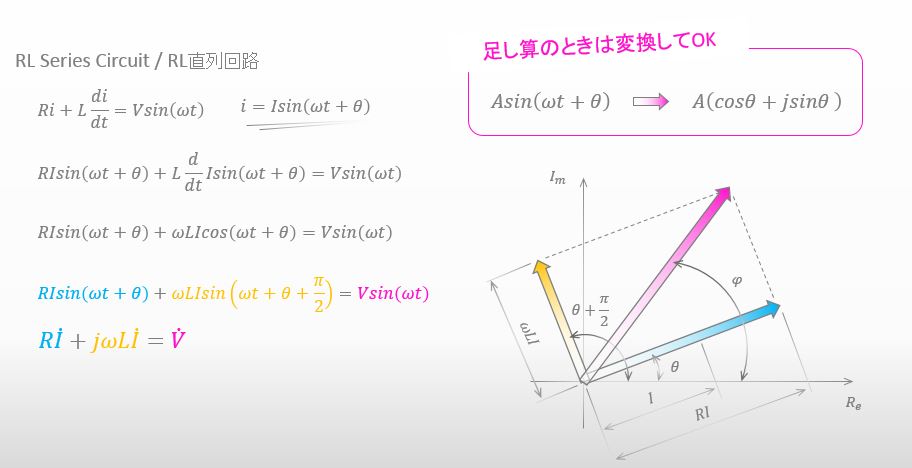
はい。で、複素数を使うと、こんな感じの計算になりますか?
![]()
いいね。正確に言うとΦ=0なんだけど、まぁいいや。この計算が言っていることは、青の複素数と黄色の複素数の足し算をすると、赤の複素数となるってことだね。そしてその赤の複素数が実は電圧と等しいんだよ ということが数式から読み取れる。
で、いま電流と電圧の関係がわかるんだけど、説明してもらっていいかい?
![]()
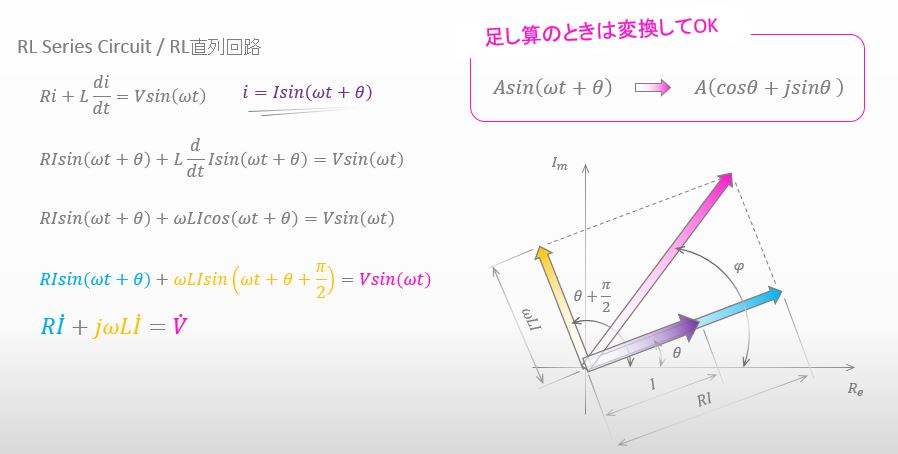
はい。電流 i を I sin(ωt+θ) と置いて計算をしているので、電流の複素数は以下の図の紫の複素数となります。
![]()
これで交流回路の微分方程式にどうやって複素数を適用しているのかは理解できたよね。
上に示した三角関数の微分方程式は、完全に複素数の問題へと帰着されたと言えるわけよ。
どんなときに三角関数を複素数に変換できるのか?
![]()
なるほど。三角関数と複素数の変換が可能なのはどんなときなのかわかった気がします。
電力を求めるときの様な三角関数同士の掛け算の場合は、掛け算を複素数に落とし込むことができない為、複素数は使用できないということですね。
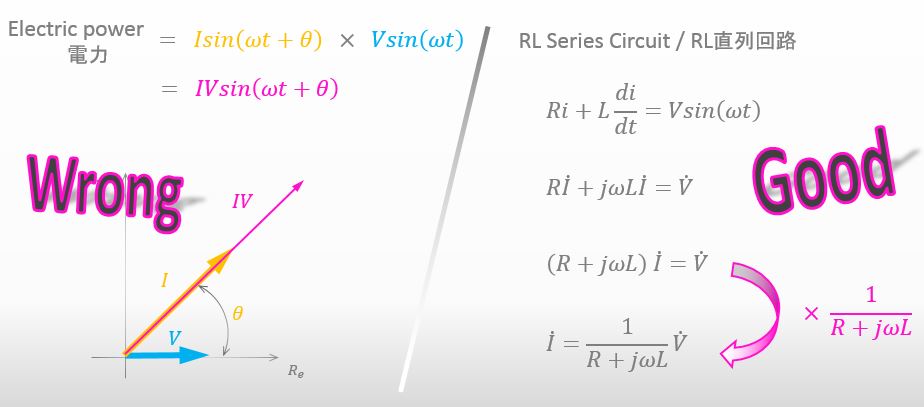
![]()
そういうこと。簡単に言うと、三角関数における線形的な計算をする場合、複素数を使えるよ って話。
![]()
助かりました。ありがとうございました。

