Get along with infinitesimal change and approximation
How to treat infinitesimal change in physics
Related articles
Contents
In a physics class
![]()
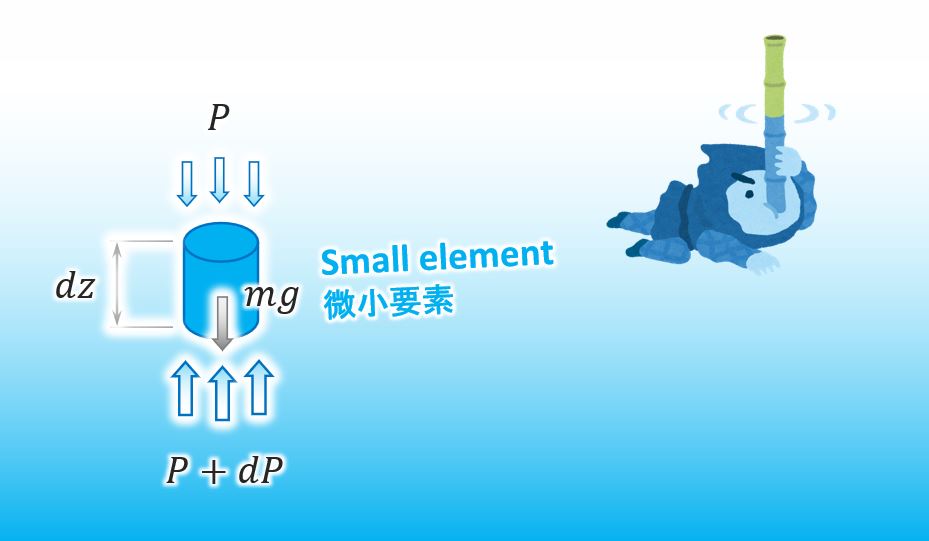
In order to find the function of water pressure, it’s the best way to analyze a small element in the water like below.

![]()
The water pressure on the bottom side is a little bit larger than the pressure on the top. We can describe the infinitesimal difference by using dP as seen below.
![]()
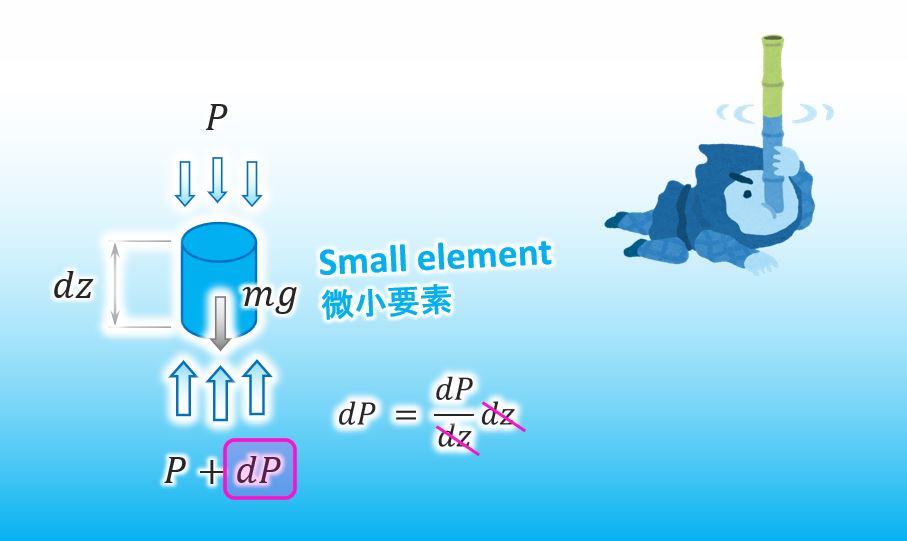
The reason why dP is the infinitesimal difference of the water pressure is that dz can be reduced like below.
![]()
And then we describe the equation of motion of the small element at zero acceleration, also known as equilibrium equation.. Oh, time is up. See you next week.
Question about approximation
![]()
Hmm…
![]()
You look like you have questions.
![]()
I’m feeling like Mr. Owl tricked me.
![]()
Why do you think so?
![]()
If I can really use Mr. Owl’s method to approximate the infinitesimal difference, I feel like I can make any equations in physics very easily.
![]()
Really?
![]()
It’s because I just add “d” to the value at a little bit far position on the infinitesimal element.
![]()
I see. First of all, I’ll give you a topic about the differential of a simple function and approximation.
Differential of a simple function and approximation
![]()
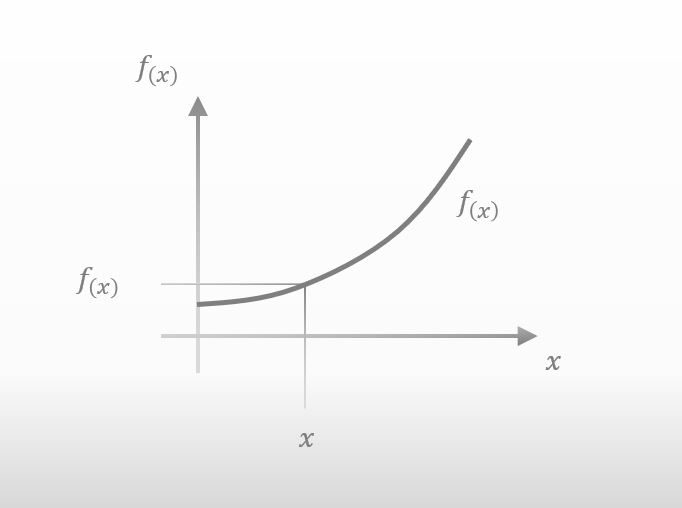
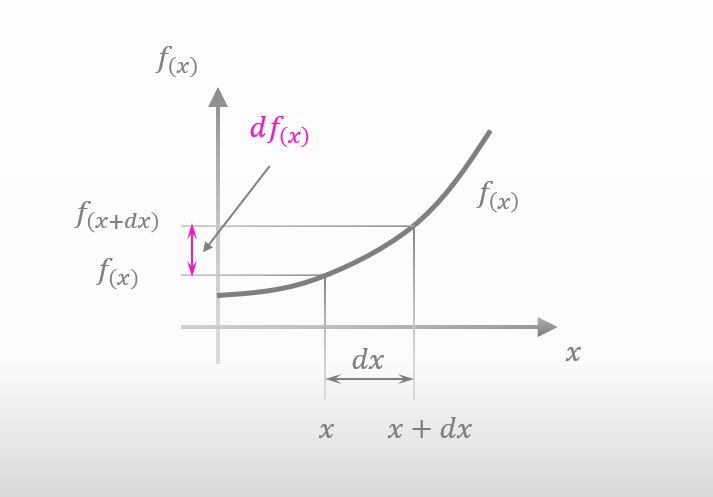
Here is a graph of f(x).
![]()
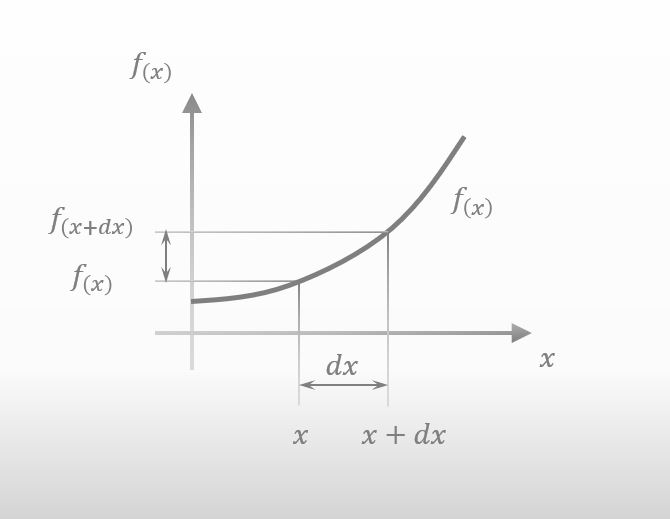
If x moves to the right only a little, f(x) also changes a little like below.
![]()
The amount of small change in f(x) is described as df(x), isn’t it?
![]()
Right. Can you approximate df(x) by using the differential of f(x)?
![]()
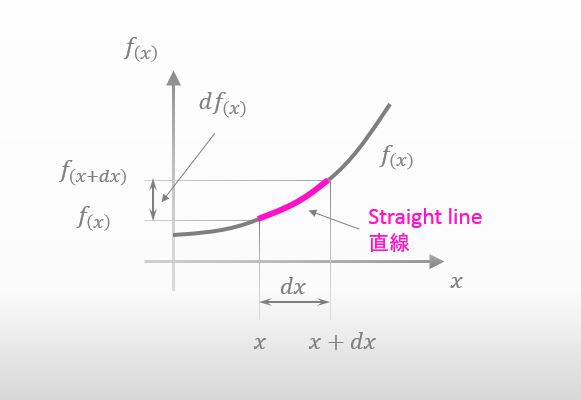
Well.. Since we consider dx as a very small value, we can regard the red curve in the figure below as “a straight line”. Am I right?
![]()
Yes. Then, can you easily find df(x)?
![]()
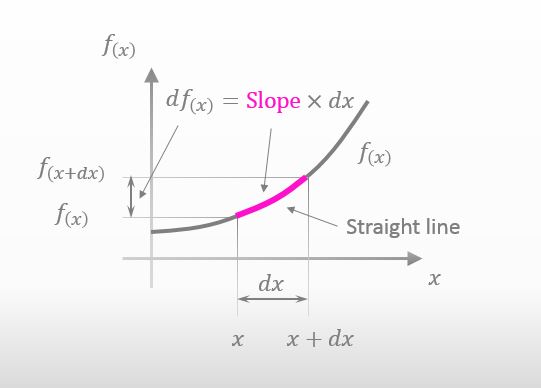
As shown below, df(x) can be expressed as “the slope of the straight line × dx”.
![]()
What is the amount of the slope of the straight line?
![]()
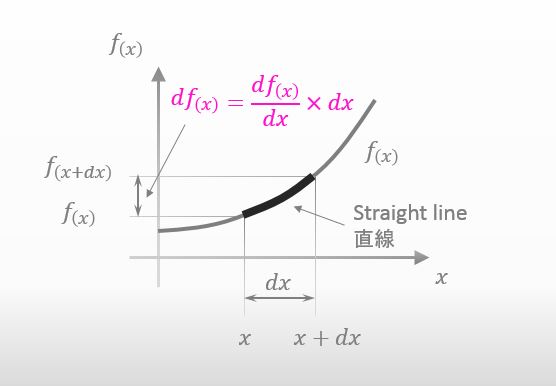
The amount of the slope is the differential of f(x). And so, we can express df(x) like below.
![]()
Right. You’ve become able to approximate how much the amount of df(x) is. If you’d like to know the details, you can google “Taylor series”.
![]()
Taylor series? I’ll check it later.
By the way, is the idea of the approximation important?
![]()
Yes, very much. Mr. Owl was going to find the function of water pressure by using the idea. The key point to find it is that he assumes something for the function of water pressure.
![]()
What does he assume?
![]()
Mr. Owl assumed that time, temperature, and other factors are nothing to do with water pressure but only water depth is relevant to water pressure in his class a while ago.
![]()
What makes the situation better if we assume so?
![]()
The approximate expression becomes simple. In other words, we can use the approximation below we found a while ago since the function has only one variable.
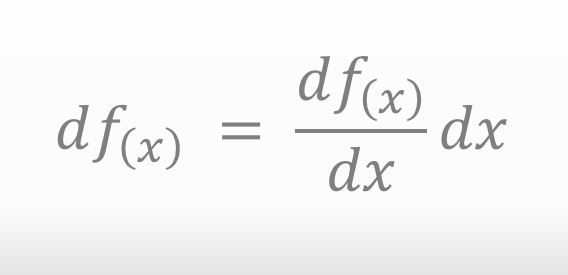
![]()
How can we approximate df if it has some variables?
![]()
You can check this lecture out. Get along with total differential and chain rule (in production..)
![]()
Thanks. I understood that we assume that the function of water pressure has only one variable and it’s water depth. How can we actually find the function of water pressure?
Let’s actually find the function of water pressure by using the way of approximation
![]()
First of all, can you draw all of forces applied to a small element in water? You can omit the horizontal forces since the forces are balanced with each other.
![]()
Sure. Here it is.
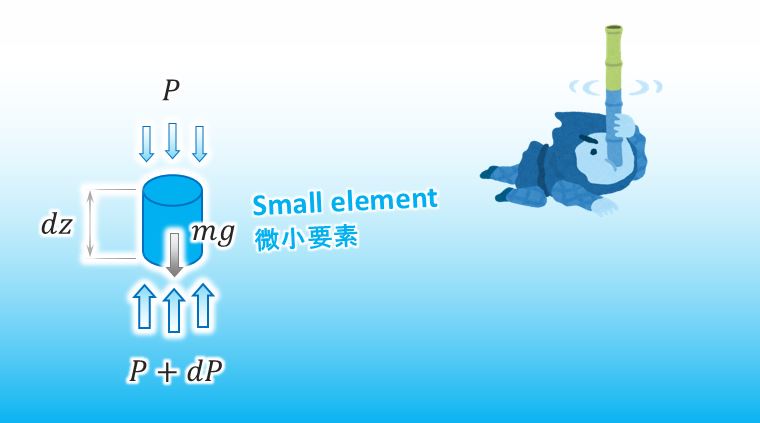
![]()
Thanks. You can approximate how much the amount of dP is, can’t you?
![]()
Yes, of course. Here you are.
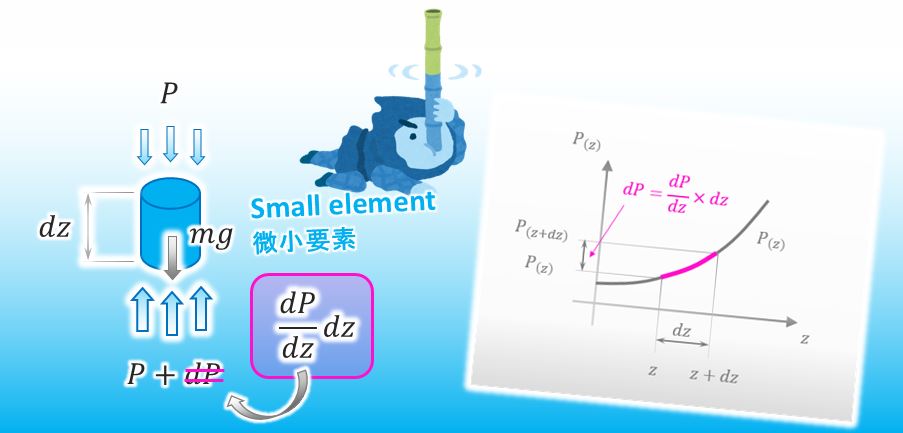
![]()
Perfect. And so, we can describe the equation of motion of the small element at zero acceleration as seen below.

![]()
I organized the equation like below. I have succeeded in deriving the function of water pressure.
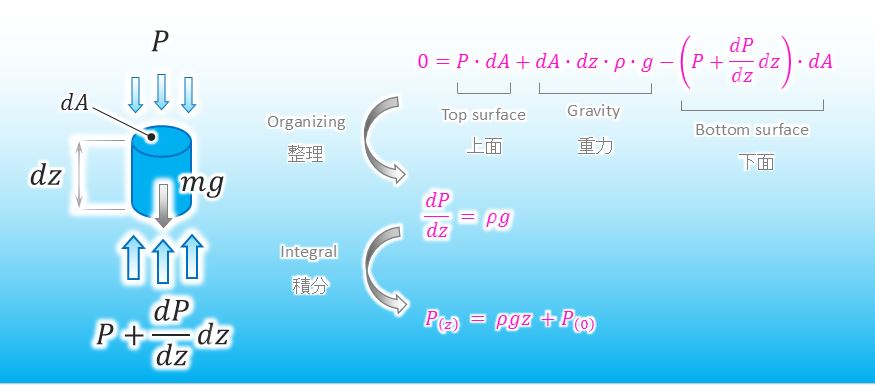
![]()
Good job. The idea of “differential and approximation” is so useful, isn’t it?
![]()
Yeah I think to. I understood it clearly.
