物理での微小変化の取り扱い方

 

 

 

 

 

 

—— 物理の授業にて ——

 

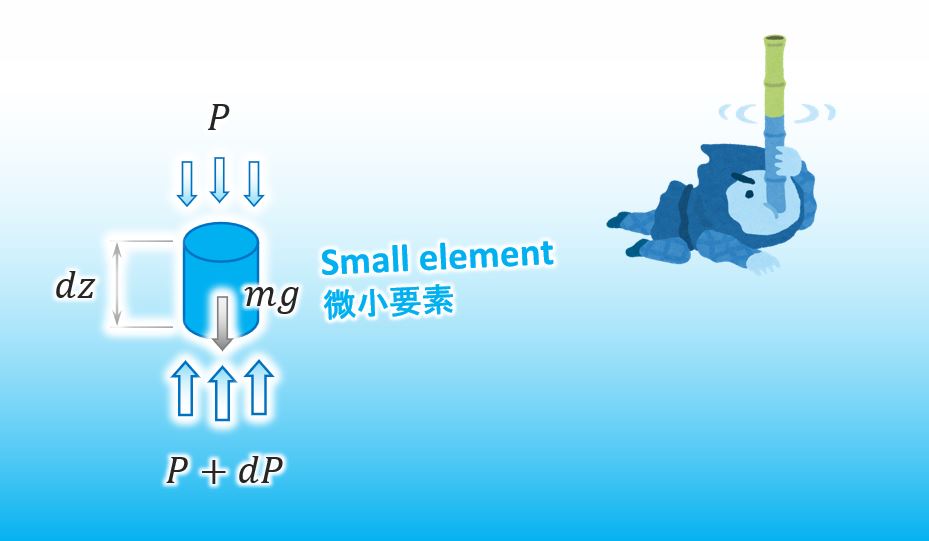
水圧の関数を求めるためには、以下の様に水中の小さな要素を考えるのが一番の方法です。

 

 

下面の水圧は上面の水圧より少し大きく、dP を使ってその微小差を以下の様に表すことが出来ます。

 

 

何故 dP が水圧の微小差になるのかというと、以下の様に dz を約分することが出来るからです。

 

 

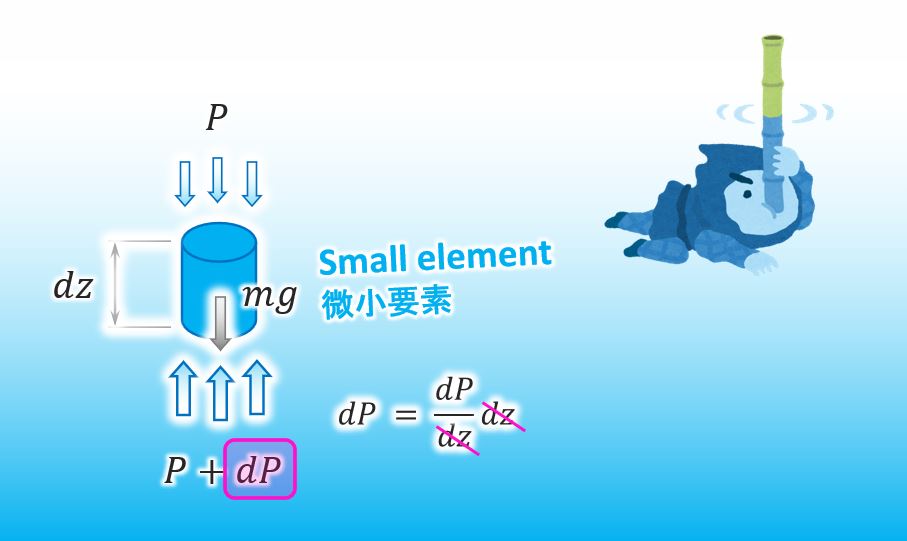
で、この微小要素に対して加速度ゼロの運動方程式、すなわちつり合い方程式を…あ、もう時間だ。ではまた来週。

 

 

近似の疑問

 

Hmm…

 

なんだか疑問が残ってる様子だね。

 

フクロウ先生に騙されている気がして。

 

何でそう思うの？

 

もし本当にフクロウ先生が言う方法で微小差を近似できるのなら、物理に関する方程式なら なんでもかんでも簡単に記述できる気がするんです。

 

そうなの？

 

だって微小要素を考えて、少し離れた箇所の値には “d” を加えて立式すればいいだけですよね。

 

なるほど。ではまず単純な関数の微分と近似に関する話を紹介しよう。

 

 

単純な関数の微分と近似

 

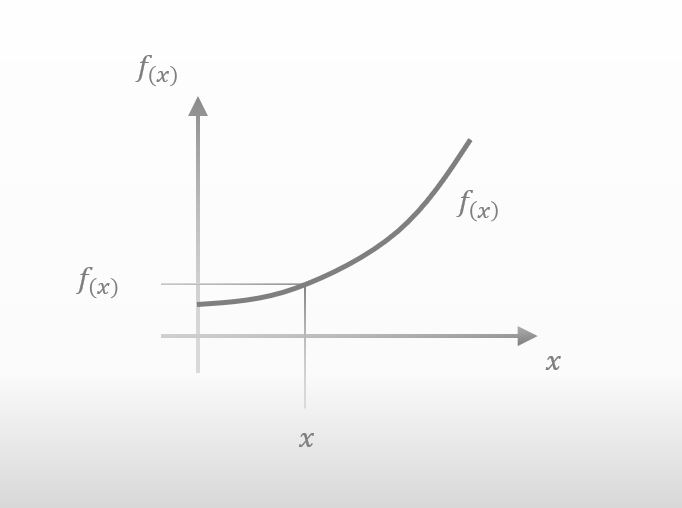
これが f(x) のグラフなんだけど、

 

 

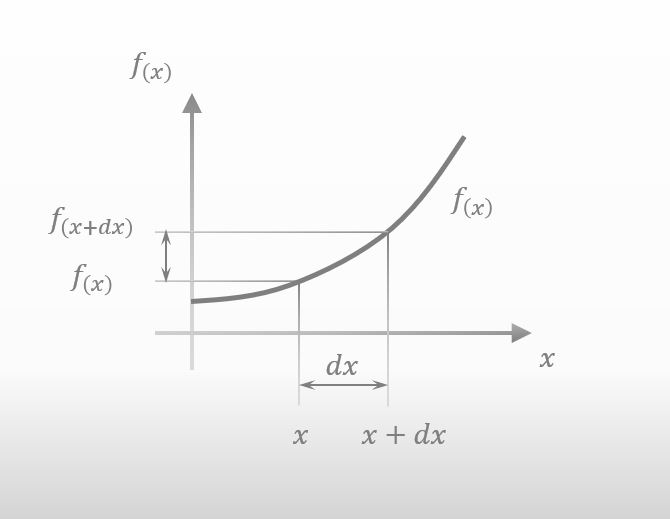
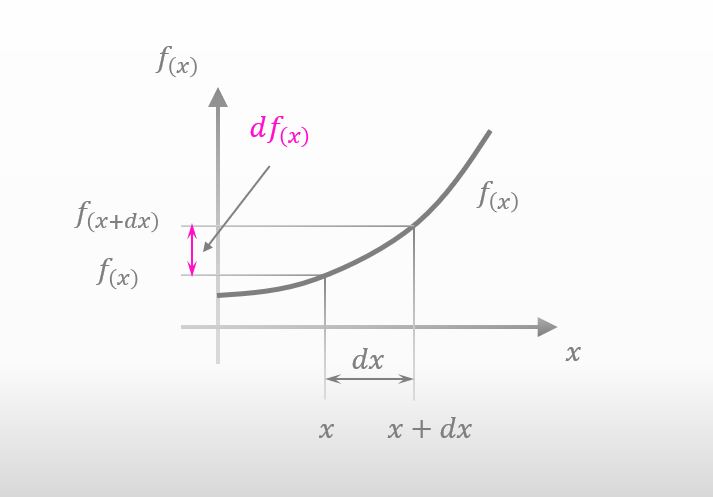
x が少し右へ移動したら、f(x) も少し変化するじゃん。下の図みたいに。

 

 

そうですね。で、その f(x) の少しの変化量は df(x) と表されるんですよね。

 

 

そうだね。したら、df(x) を f(x) の微分を使って近似できる？

 

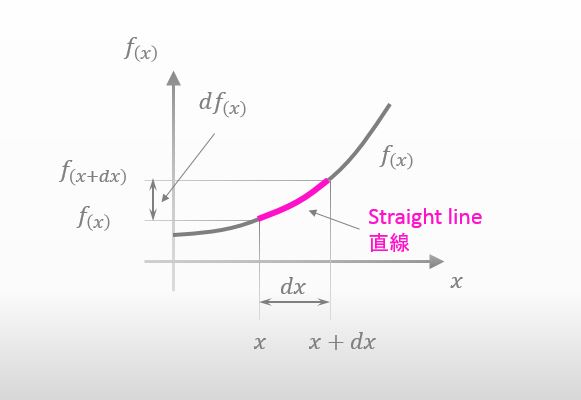
えぇっと..　dx はとても小さな値だと考えているので、下の図の赤い曲線は『直線』とみなすことが出来ますよね？

 

 

そうだね。じゃぁ df(x) は簡単に求まる？

 

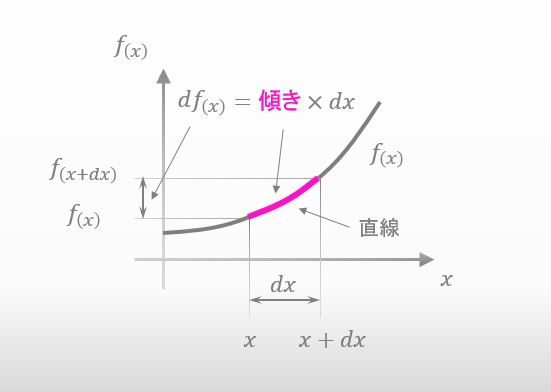
以下に示すように、df(x) は『直線の傾き × dx』と表すことができます。

 

 

その直線の傾きの大きさは？

 

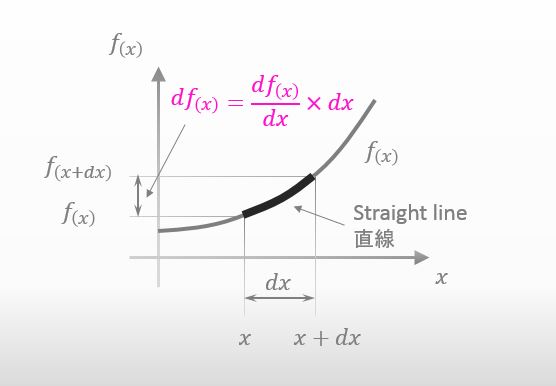
f(x) を微分したものが傾きの大きさです。そうすると df(x) は以下の様に記述することができますね。

 

 

そうだね。これで df(x) がどれくらいの量になるのか近似できるようになったね。もっと詳しく内容を知りたければ、『テイラー展開』でググってみるといいかもよ。

 

テイラー展開？　後で調べてみます。
ところでこの近似の考え方って、そんなに重要なんですか？

 

とても重要だよ。フクロウ先生はこの考え方を使って、水圧の関数を求めようとしてたんだ。このときポイントとなるのは、水圧の関数に関してある仮定をしていることなんだ。

 

どんなことを仮定しているんですか？

 

水圧は水深だけの関数だ ってこと。フクロウ先生はさっきの授業において、時間とか温度とかは関係なくて水深だけが水圧に関係している って仮定してたわけ。

 

そう仮定すると、何かいいことがあるんですか？

 

近似式が簡単になるってことだね。つまり、変数が１つだから さっき求めた以下の近似式を使えるようになるんだわ。

 

 

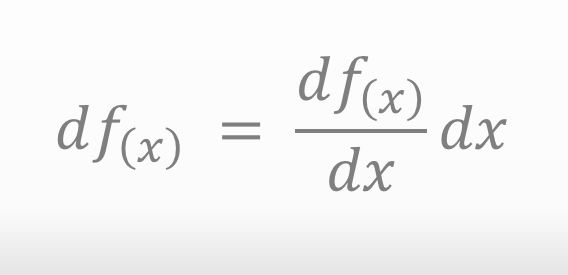
変数が複数のときはどうやって df を近似すればいいのですか？

 

この授業を見てみてよ。全微分とチェーンルールに親しむ（製作中…）

 

どうも。水圧の関数の変数が１つだと仮定している ってことを理解しました。では実際にどうやって水圧の関数を求めればいいんですか？

 

 

近似を使って実際に水圧の関数を求めてみよう

 

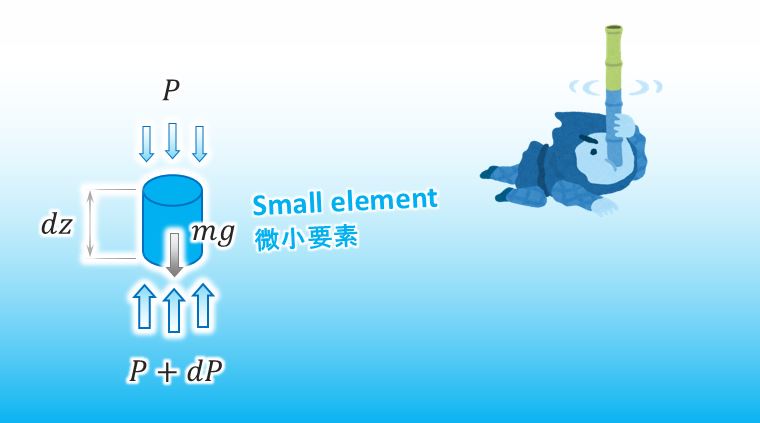
まずは、水中の小さな要素に働く力を 全部書き出して欲しいんだけど いける？水平方向の力は釣り合うんで省略していいからさ。

 

これでどうでしょうか？

 

 

どうも。で、dP がどれくらいの量になるのかは もう近似できるよね？

 

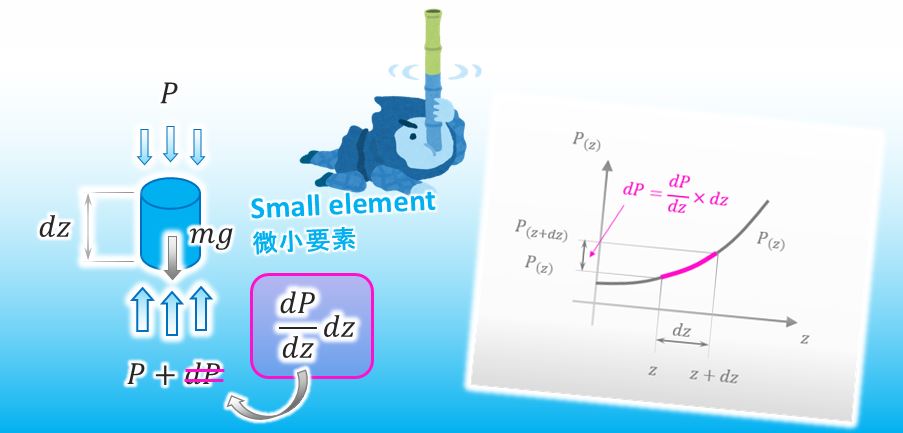
もちろんです。はいどうぞ。

 

 

完璧だね。とうことで、微小要素の運動方程式（加速度ゼロ）は以下の様に記述できるわけだ。

 

 

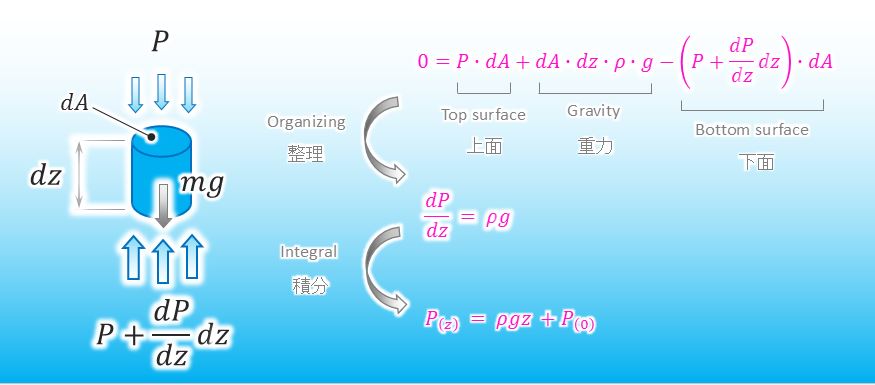
その式を以下の様に整理してみました。水圧の関数の導出に成功したと言えます。

 

 

やったじゃん。微分と近似の考え方は有効だったでしょ？

 

そうですね。ちゃんと理解できました。