Basic of fluid mechanics

 

 

 

 

 

Questions about the material derivative

 

Unlike rigid-body dynamics, fluid mechanics analyzes the movement of fluid at some fixed positions at a certain time like the figure below. In other words, a velocity is a function of time in rigid-body dynamics, while a velocity in fluid mechanics is expressed as a function of time and position.

 

 

So, we can partially differentiate a velocity with respect to time in fluid mechanics but what does the partial derivative mean? Does it mean an acceleration?

 

 

 

They say that the material derivative of a velocity of fluid is an acceleration of the fluid, but why can we say so? What is the difference from an ordinary derivative in rigid-body dynamics?

 

 

 

If you have those kinds of questions, this article will help you understand what the material derivative is. We are going into a topic about what the partial derivative of a velocity with respect to time means first.

 

 

Does the partial derivative of a velocity with respect to time mean the acceleration?

 

The figure below clearly shows what the partial derivative of a velocity with respect to time is. The time partial derivative means the time rate of change of the velocity of fluid A and the velocity of fluid B, which came into the place where fluid A left. Since the time partial derivative is the time rate of change in velocities of “different materials”, the partial derivative does NOT express the acceleration. The partial derivative is the time rate of change in velocities at a certain position.

 

 

 

Why does the material derivative of a velocity mean the acceleration?

 

As I have already told in this article, a velocity in fluid mechanics is expressed as a function of time and position like in the figure below. It’s because fluid mechanics observes many fluid particle at the same time at a certain time.

 

 

 

Then, how can we know the acceleration of fluid in fluid mechanics expression. We need to observe the movement of one fluid particle like what we find an acceleration in rigid-body dynamics. Since we observe the movement of one fluid particle, we can’t think that time and position are indipendent parametes. We need to think that time and position are related with each oter. In other words, we need to think that position vector is a function of time.

 

 

 

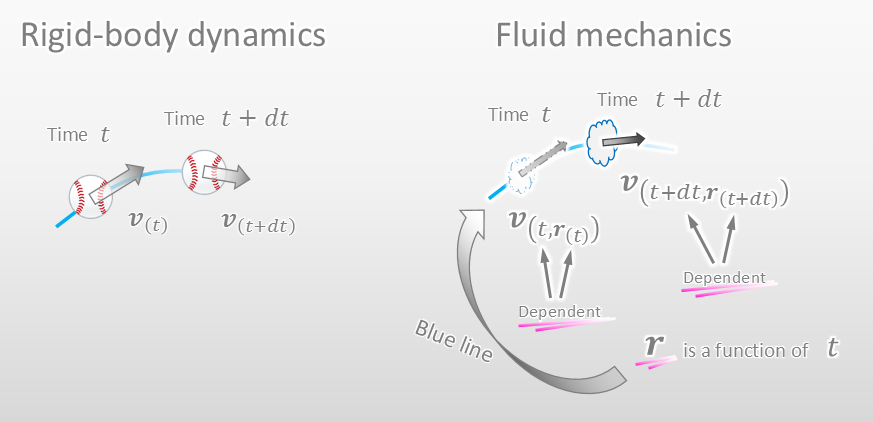
Now you can easily find the acceleration of fluid. Please take a look at the figure below.

 

 

 

I’d like you to pay attention to only x component since there is no space on the screen. In order to differentiate it, we can apply “chain rule” to it.

 

 

 

Did you realize something? Actually, the last expression is the material derivative.

 

 

 

I hope this article helped you understand the reason why the material derivative of a velocity means the acceleration.