物質微分って何?
流体力学の基礎
物質微分の疑問
流体力学では剛体/質点の力学とは異なり、以下の図の様にある時刻にある場所での流体の動きを観察します。つまり剛体/質点の力学において速度は時刻の関数でしたが、流体力学では速度は時刻と位置の関数として表現されます。
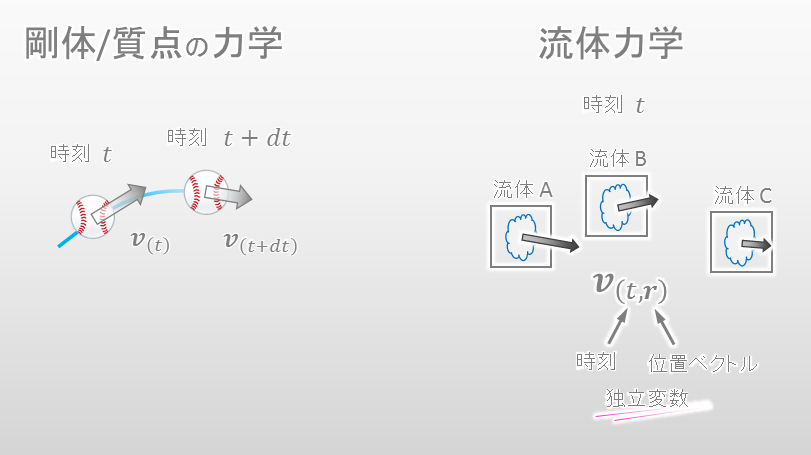
では、流体力学において速度の時間偏微分は何を表すのでしょうか?加速度でしょうか?

速度の物質微分が流体の加速度なのだそうですが、なぜなのでしょうか?また、剛体/質点の力学における加速度とは何が違うのでしょうか?

同じような疑問を持たれた方は、引き続きこの記事をご覧ください。というわけでまずは速度の時間偏微分が何を意味しているのかを考えてみましょう。
速度の時間偏微分は加速度を意味するのか
以下の図を見ると明らかですが、速度の時間偏微分というのは、ある場所における流体Aの速度と、dt秒後にその場所に流入した流体Bの速度の時間変化率を表現しております。『異なる物質』の速度変化を意味しておりますので、速度の時間偏微分は流体の加速度ではないことがわかります。速度の時間偏微分は、とある場所における速度の時間変化率を表現しているだけです。
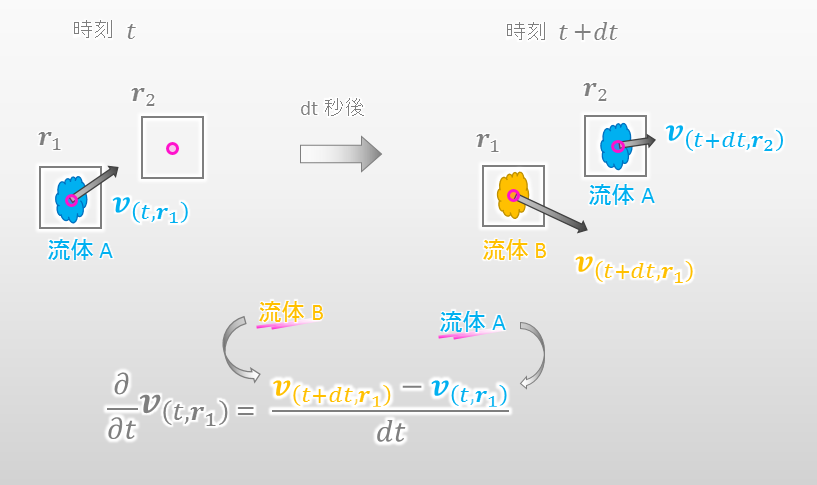
速度の物質微分はなぜ加速度を意味するのか
この記事内で既に述べたように、流体力学では以下の図の様に速度は時刻と位置の関数として表現されます。なぜなら、流体力学ではある時刻に様々な流体粒子を同時に観察する為です。

そうすると、流体力学の記述法で流体の加速度を知るにはどうすればよいでしょうか。剛体/質点の力学と同様に、ひとつの流体の動きを観察する必要があります。ひとつの流体の動きを観察するので、時刻と位置はもはや独立変数ではなく、互いに関係しあっている変数として考える必要があります。つまり、位置ベクトルは時刻の関数として考えるということです。
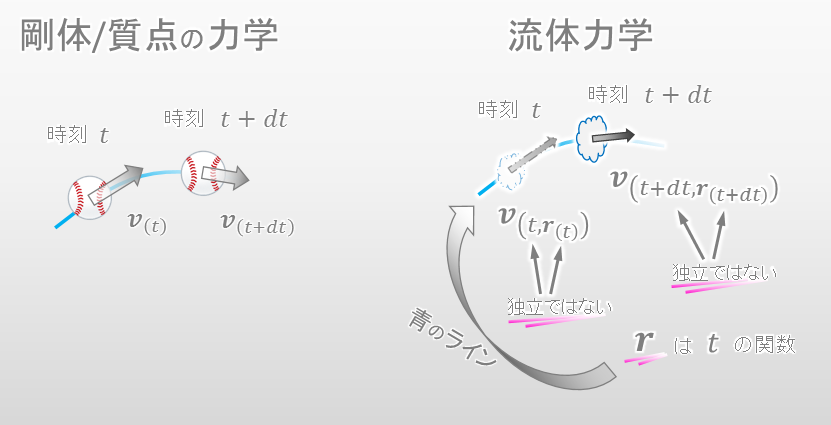
ここまで理解できればあとは簡単です。実際に加速度を求めてみましょう。
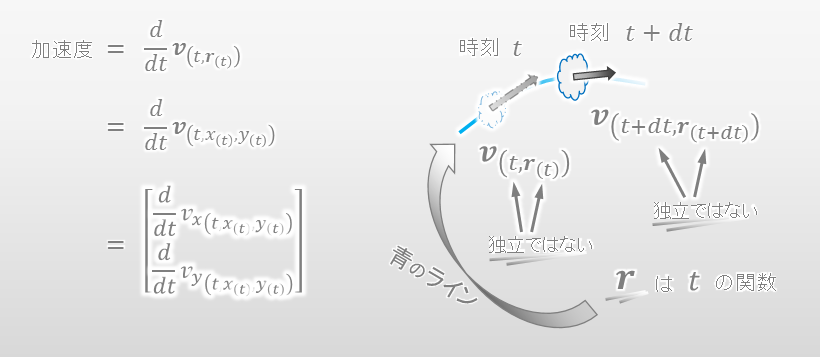
x成分のみ計算してみます。連鎖律(チェーンルール)を使って微分すると、以下の様に加速度を計算することができます。
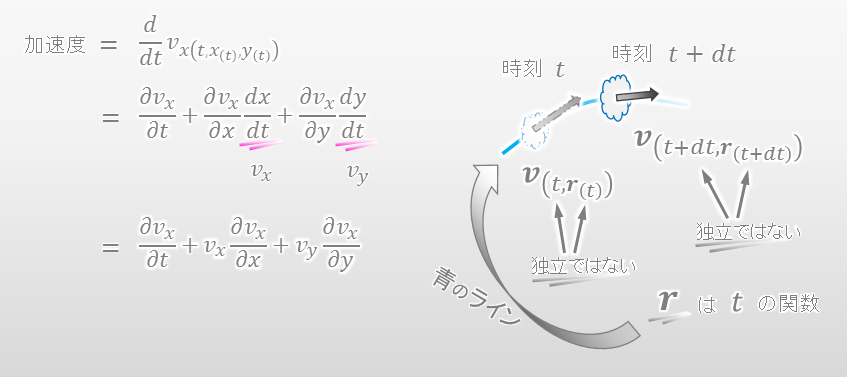
何か気付いたことはありますか?実は、最後の式は物質微分そのものです。
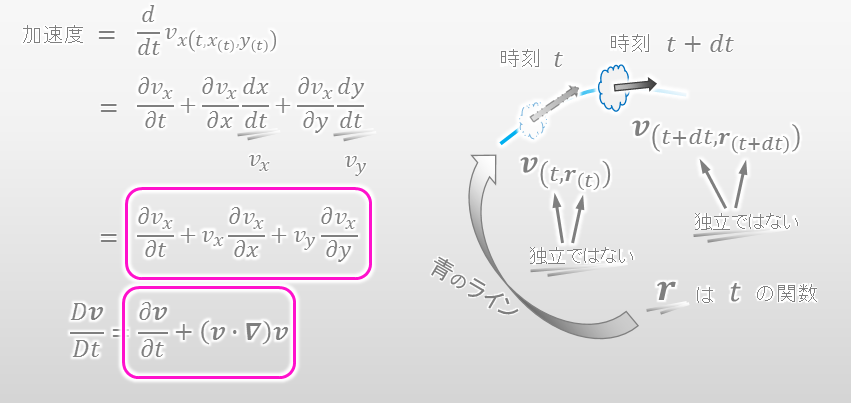
速度の物質微分が加速度を意味する理由は理解いただけたでしょうか?

