Yielding of a material and a stress tensor

 

Mr. Penguin, what is Mises Stress? I have no idea about it. I’d like to get an overview of it.

 

Okay, I’ll provide an overview of Mises Stress. I just prepared a material for you. Will you give a tension to it?

 

Sure. Ah, the material got broken when I applied 1000[N] to it.

 

 

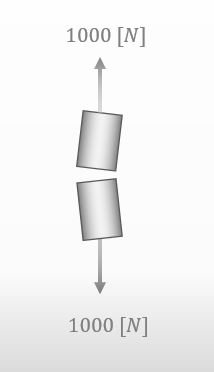
I see. Then I will prepare the same material again.

This time, I apply a little horizontal forces to it. If you give a tension in the same way as you did a while ago, do you think the material will get broken with 1000[N] again?

 

 

No. I guess that the material will get broken with a different force from 1000[N] since the situation is different.

 

Right. When you design a machine, you have to know whether a material will get broken or not even though many different kinds of forces are applied to the material like the figure below.

 

 

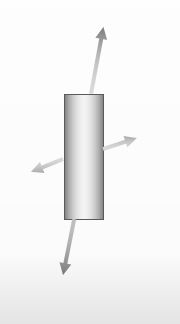
In other words, when the stress tensor at a point in a material is given like the figure below, we’d like to know whether the stress tensor meets the conditions to yield or not.

 

 

 

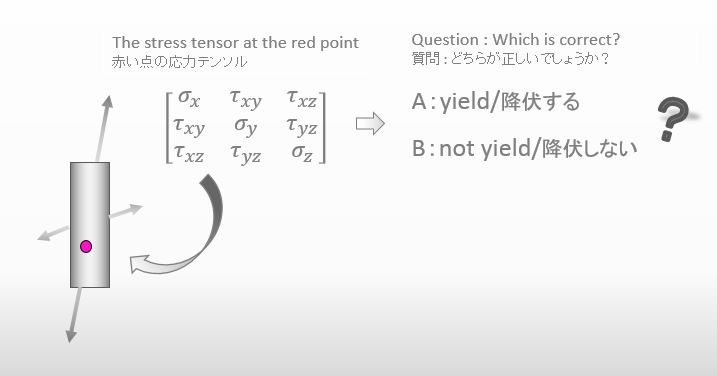
Outline of a stress tensor

 

Just a minute… Would you tell me what a stress tensor is first..?

 

Hahaha… Okay, I’ll explain it briefly. By the way, we already learned tensors in “What’s the difference between a tensor and a matrix？“. You can check it out.

Let me give you a question. Can you answer if I ask you to find the stress value at the point below?

 

 

The stress value?? I’m afraid but I can’t get the meaning…

 

Actually, your answer is correct.

Nobody can answer the question like “the stress value at the point is 10[MPa]”. Let me change the question. Can you find the “stress vector” at the point?

 

Since a stress vector depends on the direction of a surface, we need to define the direction of a surface first like the figure below. We can find the stress vector only after the direction of a surface is defined.

 

 

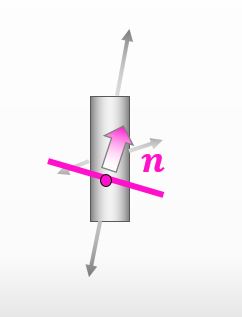
Great. Then lets’ say the direction of the surface is given. How can we find the stress vector?

 

As I showed in the figure below, we can find the stress vector by multiplying the stress tensor at the point by the direction of the surface.

 

 

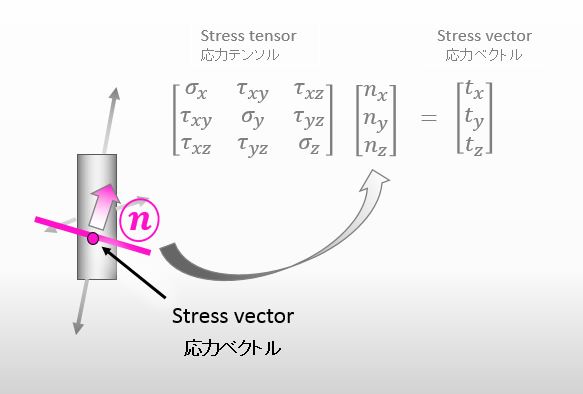
Wow.. You understand well. A stress tensor is so useful, isn’t it?

What I’d like you to keep in mind to help you understand this lecture is that you can figure out everything about applied forces to the point in the material if you know the stress tensor at the point.

By the way, I’d like you to take a look at the figure below. Did you know that the values of the components of a stress tensor depend on a coordinate system?

 

 

 

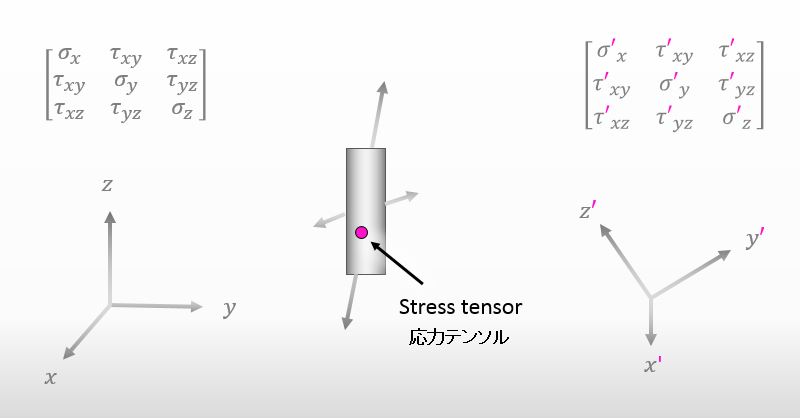
Relation between yielding and a coordinate system

 

Yes, but is it important right now??

 

Actually, Mises stress makes use of it.

 

How? Or rather, I’d like to know what Mises Stress is like first..

 

To put it simply, Mises stress is an evaluation function for us to know whether a material will yield or not.

Please take a look at the figure below. If you input the components of a stress tensor, the function, which we call Mises stress, outputs a value. And then you can evaluate whether the material will yield or not with the amount of the outputted value.

 

 

I see. But why can the function called Mises stress evaluate whether a material will yield or not?

 

I’ll tell you about it. Firstly, can you agree whether a material yields or not doesn’t depend on a coordinate system?

 

Yes, I can agree. There is no way a material yields only with a specific coordinate system. The material doesn’t know about coordinate systems.

 

 

 

Yup. Then let’s find a function whose value of an output doesn’t change with coordinate systems.

 

 

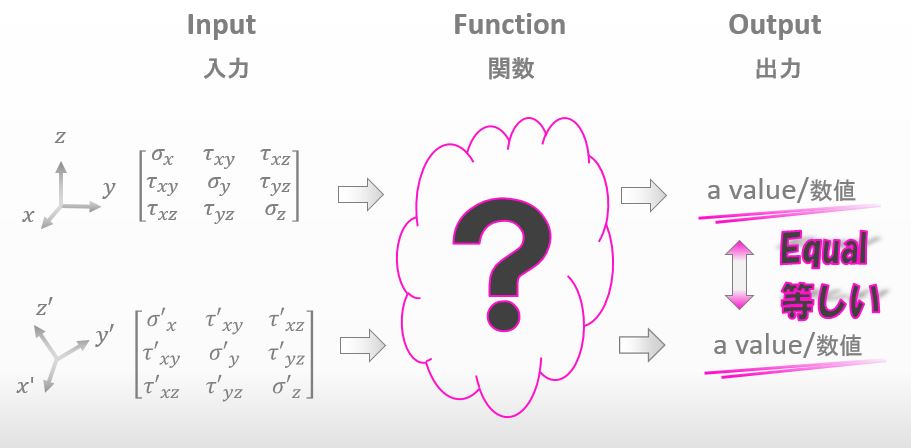
If there is the only function in the world that outputs the same value with any coordinate system, we can make use of it for us to find Mises stress.

 

You are right but unfortunately, there are some functions that output the same value with any coordinate systems.

That’s why Mr. Mises added two conditions regarding yielding of materials in order to define Mises stress.

 

What are the two conditions?

 

One is that each of static pressure and isotropic tension doesn’t affect material yielding. The other is that yield stress doesn’t depend on whether it’s compressive stress or tensile stress.

 

Hmm… I can’t understand that clearly.. Are the conditions really correct based on mechanics of materials?

 

It depends on a material. I mean, if you consider that you can’t apply the conditions to the material, you must not use Mises stress. Some materials can’t be applied to Mises stress.

The details won’t be part of this lecture. May be some other time. I’ll introduce how to find Mises stress a little this time.

 

 

How does Mises stress hold up?

 

I don’t like thinking in a difficult function. Assuming that the function that meets the two conditions of Mises was simple like the function below, could you show me how we can find Mises stress?

 

 

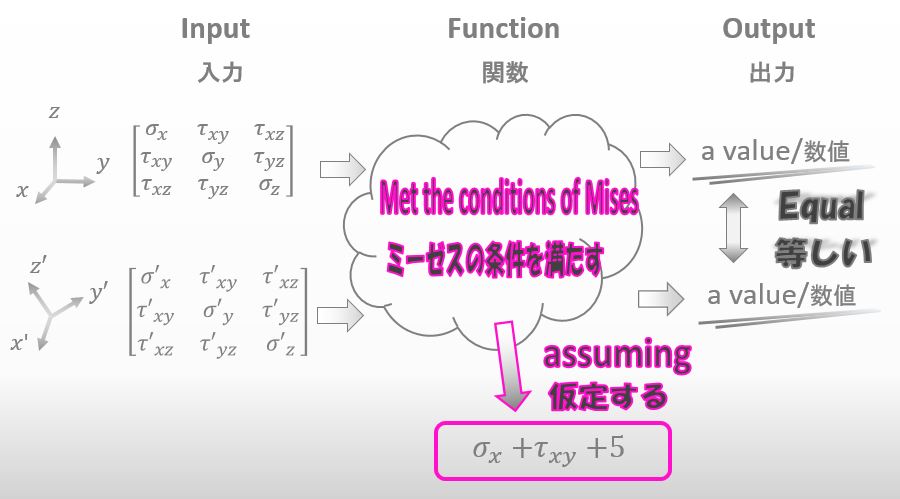
Okay, let’s assume that the function was the one you said.

Let’s say you carried out tensile testing and it turned out that the yield point of the material is σ[MPa]. Can you describe the stress tensor when the material started yielding?

 

Is this correct?

 

 

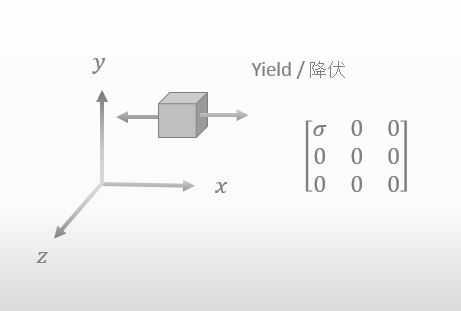
Right. Then will you substitute the components of the stress tensor into the function that you assumed?

 

Sure. Here it is. I substituted σ for σx and substituted zero for τxy.

 

 

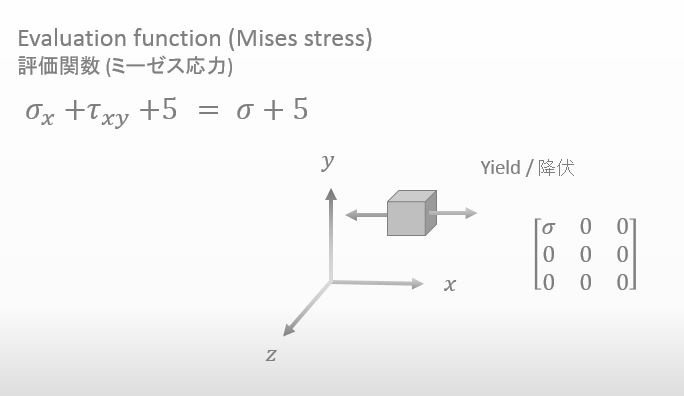
Good. Then will you solve the equation for σ?

 

It’s also easy. Here it is.

 

 

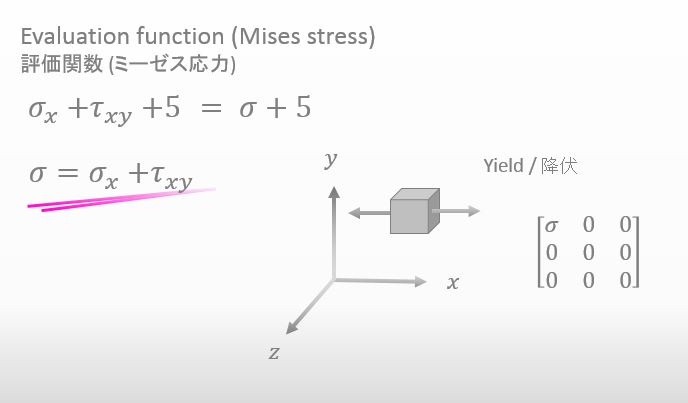
That’s Mises stress. If you calculate σx+τxy, you’ll be able to know whether the material will yield or not because we conducted tensile testing and we’ve already known that the material yields at σ[MPa].

If the result of σx+τxy is larger than σ, the material will yield.

 

Could you show me the genuine formula of Mises stress?

 

Here is Mises stress.

 

 

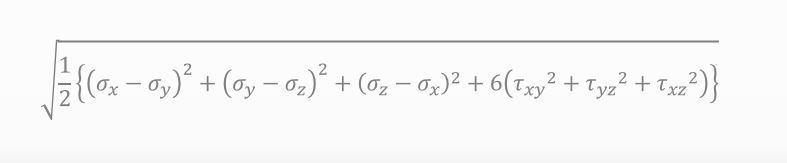
It looks complicated but it is actually useful. I just substitute the components of a stress tensor into the formula if I’d like to know whether the point will yield or not.

 

Exactly. You’ve got the overview of Mises stress. Let’s call it a day. See you.