ミーゼス応力の雰囲気をつかむ
関連記事
Contents
材料の降伏と応力テンソル
![]()
ペンギン先生、ミーゼス応力って何でしょうか?全くわからないので、雰囲気をつかみたいんですけど
![]()
教えてあげよう。とりあえず材料を準備したんだけど、引張ってみてくれる?
![]()
はい。あ、1000[N]かけたら材料が壊れちゃった。
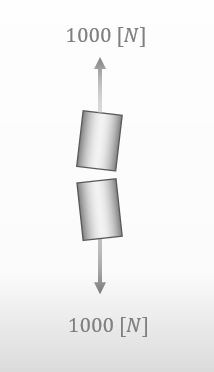
![]()
なるほど。じゃぁもう一度同じ材料を準備するわ。
今回は、私が水平方向に少し力を加えておくね。もしも君が先程と同じように引張ったら、やっぱり1000[N]で材料は壊れると思う?

![]()
いえ。状況が違うので、1000[N]とは異なる力で壊れるんだと思いますけど。
![]()
そうだね。機械を設計するときには、以下の図みたいに様々な力が材料に働いている状況下で、材料が壊れるのか否かを見極めなければならないわけよ。
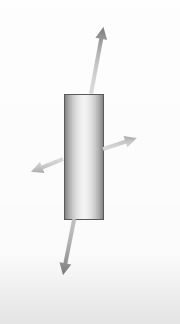
![]()
言い換えると、下図に示した様に ある点の応力テンソルが与えられたとき、その応力テンソルが降伏する条件を満たすのかどうかを知りたい わけなんだわ。
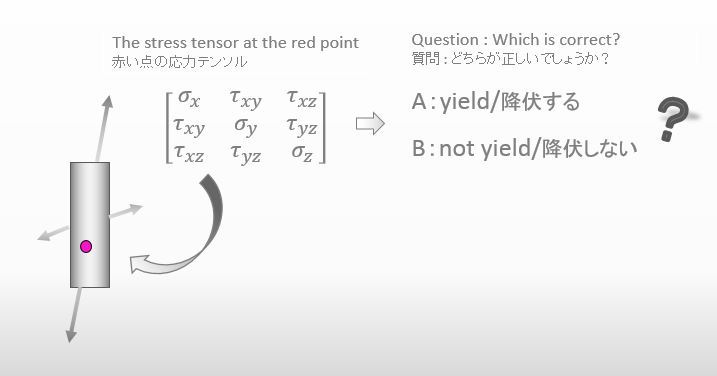
応力テンソルの概要
![]()
あ、ちょっと待ってもらっていいですか? 応力テンソルって..何でしたっけ?
![]()
それじゃぁ簡単に説明するわ。ちなみに テンソルに関しては『テンソルと行列の違いって何?』で既に学んでるから チェックしてみて。
話を戻して、もしも「以下の点の応力値を求めよ」と聞かれたら答えられる?

![]()
応力値ですか? すみませんが おっしゃっている意味がわかりません…
![]()
実は、その答えで合っているんだ。
「その点の応力値は10[MPa]です」みたいに答えることは出来ないのよ。じゃぁ質問を変えて、その点の『応力ベクトル』を求めることは出来る?
![]()
応力ベクトルって面の方向によって変わりますよね。なのでまずは下図の様に 面の方向を定義する必要があります。面の方向が決まって初めて 応力ベクトルを求めることができます。
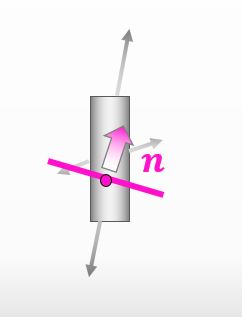
![]()
素晴らしい。では面の方向が与えられたとして、どうやって応力ベクトルを求めることが出来るかな?
![]()
下図のように、その点の応力テンソルと面の方向を掛け合わせたものが応力ベクトルになります。
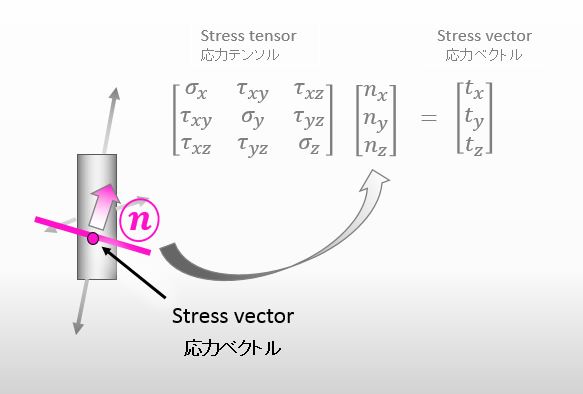
![]()
ほうほう。よく理解してるね。応力テンソルって便利でしょ?
この授業において覚えておいて欲しいことは、その点における応力テンソルがわかれば、その点に働く力関係の全てを把握できる ってこと。
ところで、下の図を見て欲しいんだけど、応力テンソルの成分は、座標系によって値が異なることは知ってる?
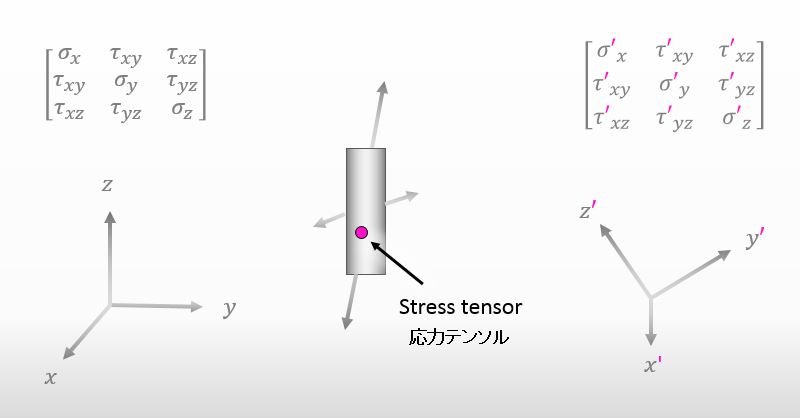
降伏と座標系の関係
![]()
知ってますけど、そのことって いま 重要なんでしょうか?
![]()
実はミーゼス応力はそのことを利用してるのよ。
![]()
どうやって? というかミーゼス応力って何なのかを教えて欲しいんですけど。。
![]()
簡単に言うと、ミーゼス応力っていうのは材料が降伏するかどうかを知る為の評価関数 なのよ。
例えば、下図みたいに、応力テンソルの成分を ミーゼス応力と呼ばれている関数に代入すると、ある数値がひとつ出力されて、その出力された数値の大小で材料が降伏するか否かを判断するわけ。

![]()
なるほど。で、何でそのミーゼス応力っていう関数は 材料が降伏するか否かを判断できるんですか?
![]()
これから話すよ。まず、材料が降伏するか否かは 座標系によらない ってことはわかるかな?
![]()
はい。理解できます。ある座標系では降伏するのに、別の座標系で考えると降伏しない なんてことはありえません。

![]()
そうだね。じゃぁまずは座標系が変わっても出力される値が変わらない関数を考えてみようか。
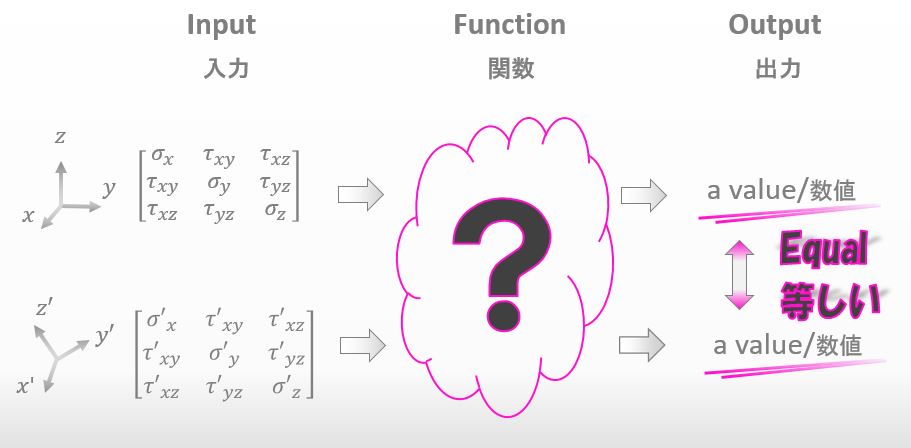
![]()
もし どの座標系でも同じ値を出力する関数がこの世にひとつだけなら、その関数を利用してミーゼス応力をつくれるわけですね。
![]()
そうなんだけど、残念なことに、そういう関数はいくつかあるのよ。
なのでミーゼスさんは降伏に関する条件を2つ付け加えて、ミーゼス応力をつくったってわけ。
![]()
その2つの条件って何でしょうか?
![]()
静水圧と等方引張は降伏に影響しない ということと 降伏応力は引張でも圧縮でも同一である ということ。
![]()
ん〜、、よくわからないですけど、その条件は材料力学的に言って本当に正しいんでしょうか?
![]()
それは材料によるね。どういうことかというと、もしその条件が適用できないと思うのであれば、ミーゼス応力をつかっちゃだめ ってこと。適用すべきでない材料もあるからさ。
まぁ詳しい話はまたの機会にしようか。今回は、ミーゼス応力の求め方をちらっと紹介しておくわ。
ミーゼス応力の成り立ち
![]()
小難しい関数で考えたくないので、ミーゼスの2つの条件を満たす関数が以下の様な簡単な関数だったとして、ミーゼス応力の求め方を教えていただけますか?
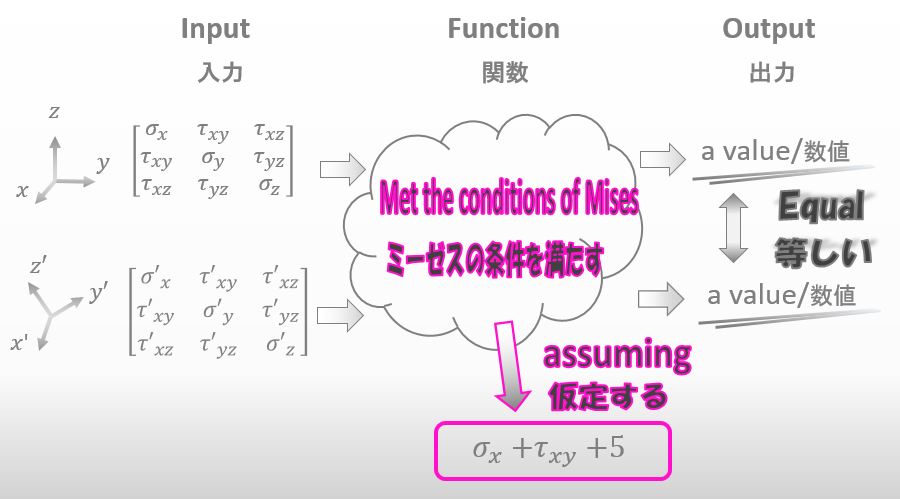
![]()
まぁいいや。その関数だったと仮定しよう。
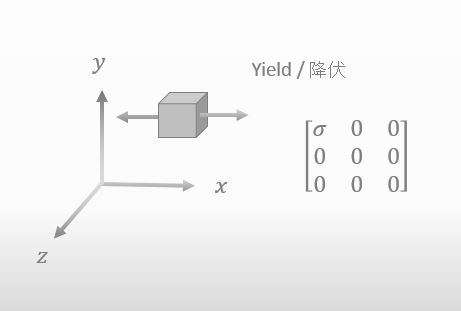
では質問なんだけど、引張試験をして 材料の降伏点がσ[MPa]だとわかったとする。降伏したときの応力テンソルがどんな値をとるかわかる?
![]()
これで良いでしょうか?
![]()
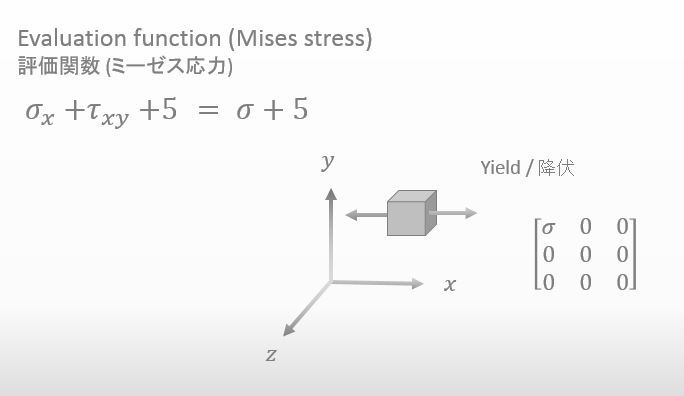
そうだね。それじゃぁその応力テンソルの成分を、さっき仮定した式に代入してみようか。
![]()
こんな感じでしょうか? σ を σx に代入して、ゼロを τxy に代入しました。
![]()
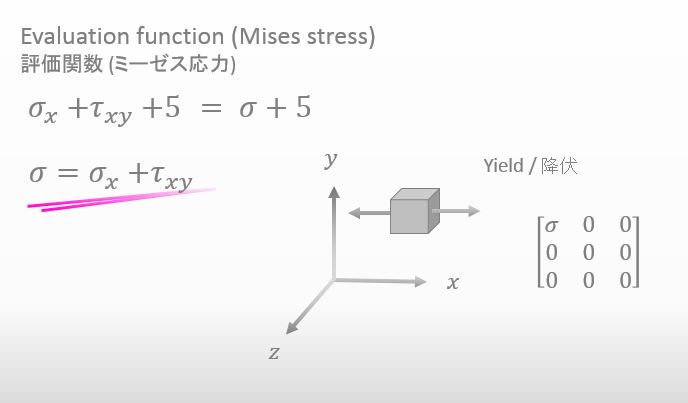
いいね。じゃぁ今度は、その式を σ に関して解いてみて。
![]()
それも簡単ですね。これでどうでしょうか?
![]()
それがミーゼス応力だよ。 σx+τxy を計算すれば、材料が降伏するか否かを知ることができる。なぜなら 引張試験をして σ[MPa] で材料が降伏する ってことを既に私たちは知っているからね。
σx+τxy を計算して、その結果が σ より大きければ降伏するってこと。
![]()
ミーゼス応力の本当の式はどんな形なんですか?
![]()
これがミーゼス応力ってやつよ。
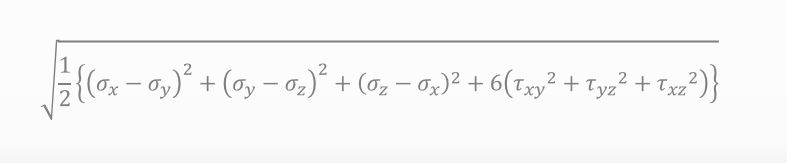
![]()
なんだか複雑だけど、要は 応力テンソルの成分をこの式に代入すれば、材料が降伏するかどうかわかる ってことですね?
![]()
その通り。んじゃぁこれで用事は済んだね。ではこの辺で。
