回転行列を30秒で導出

 

 

困ったなぁ

 

どした？

 

あ、ペンギン先生。回転行列が何で以下の式になるのかを知りたいんですけど…

 

 

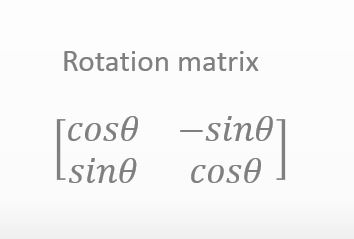
調べてみたウェブサイトはどれもこれも計算量が多すぎて嫌になっちゃいました..

 

そうなの？回転行列なんて30秒で導けるけど。

 

マジですか。早く教えてください。

 

ええよ。んじゃぁまずは、下図の２点の座標を教えてみて。

 

 

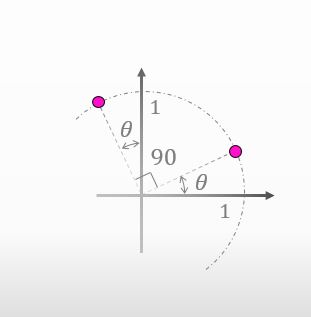
それは簡単です。はいどうぞ。

 

 

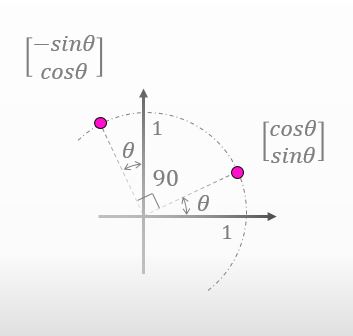
いいね。実はこれらの点は回転行列Rを使って別の形式で表現することもできるんだ。ちょいと下の図を見てみて。

 

 

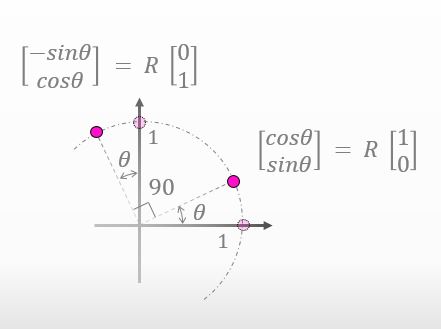
回転行列Rがどんな値かはまだわからないけど、回転行列Rを使って表現するとすれば　確かにそうも表現できますね。

 

じゃぁ次のステップに行くね。

下図の右側において、ある点 [x,y] を Φ だけ回転させたんだけど、回転後の点の座標に関して特に疑問はないよね？

 

 

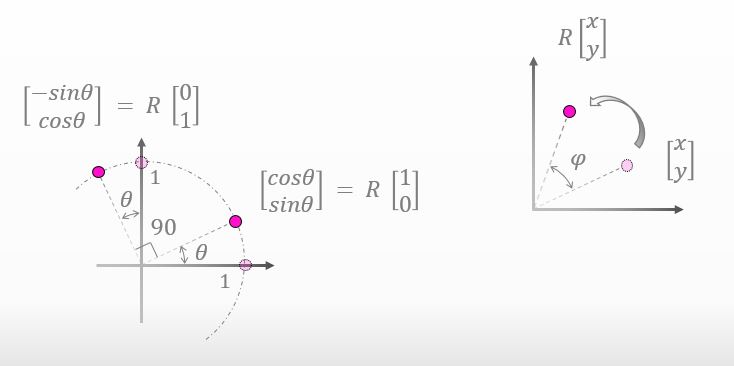
まぁそれが回転行列の意味ですから。（その回転行列Rの値がわからなくて困っているんですけど…）

 

下図の右下に式を追記したんだけど、回転させた点の座標をちょいとバラしてみた。これも疑問はないよね？

 

 

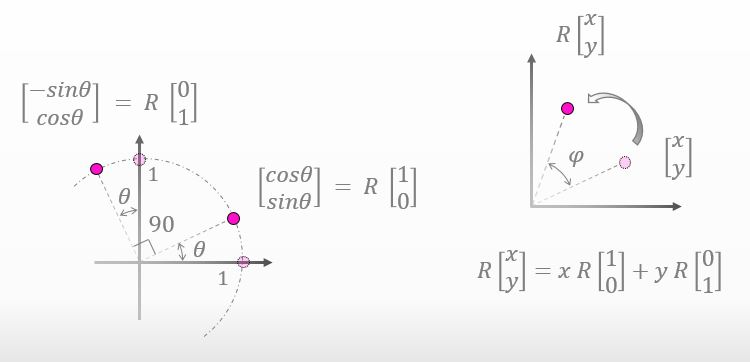
何も疑問はありません。ただR[x,y]を展開しただけですし。

 

ところで、R[1,0] と R[0,1] の値はもうわかってるんだけど、知ってた？

 

え？あっ、ほんとだ。赤枠の中がその値ですよね。

 

 

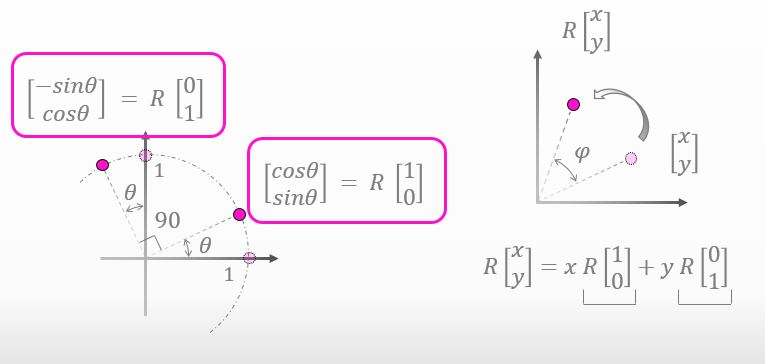
それらを上図の右下の式に代入してみ。

 

承知いたしました。これでどうでしょう？

 

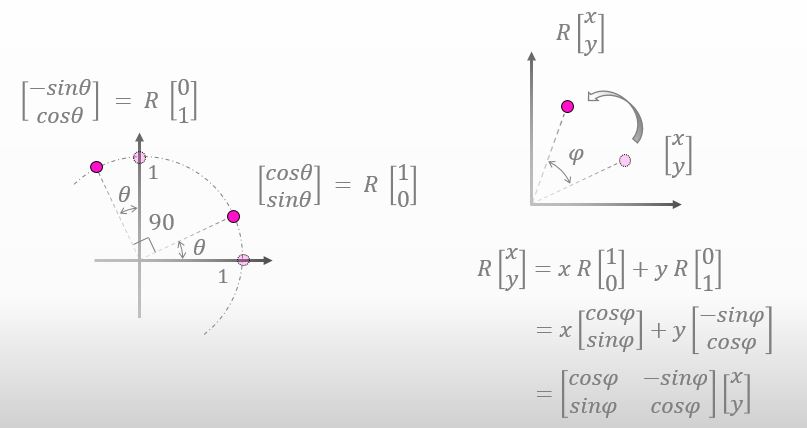
何か気付くことある？

 

いえ… 特に何も気付きませんけど..

 

そう？　さっき君が導いた式にもうちょい注目してみてよ。

 

 

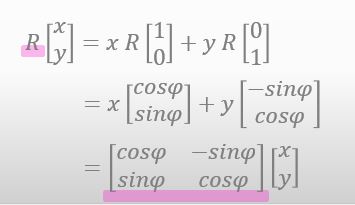
ほんとだ…　いつの間に回転行列の値が..

 

んじゃぁ、そういうことで。

 

ありがとうございました。