Strain -Get a deeper understanding of it-
Get along with “strain” more
Related YouTube video
Contents
Can you really find a very simple strain?
![]()
Mr. Penguin, I learned strain in a lecture of strength of materials today.
![]()
That’s good. How was it?
![]()
It was very easy. If I apply a tension to a material and it stretches a little, the strain is calculated like below.
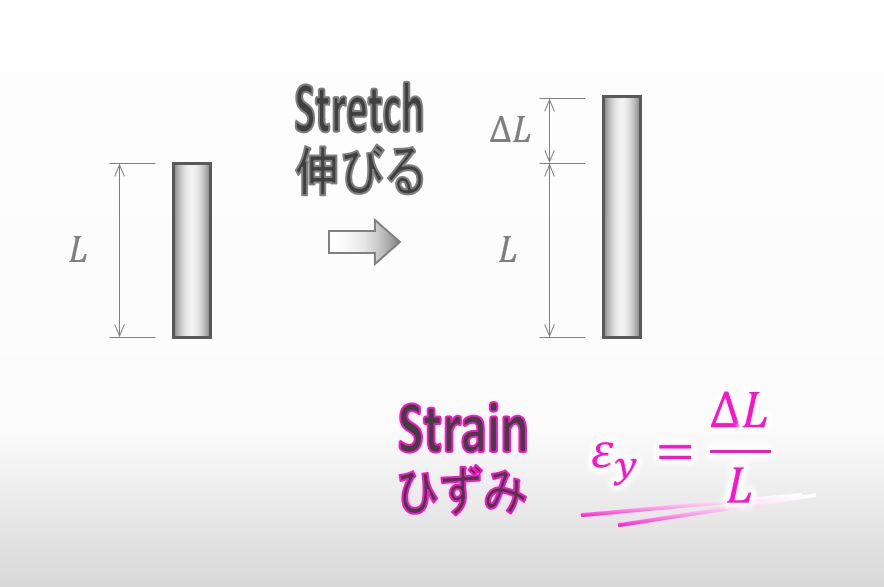
![]()
Right.
![]()
I also learned shear strain. If a material is deformed toward shear direction, the shear strain is calculated like below.

![]()
Is there anything else you know?
![]()
The strains I’ve been talking about were called “engineering strain”. There is another way to express strain. That is “strain tensor”.
![]()
Will you explain the relation between engineering strain and strain tensor?
![]()
Sure, it’s easy to explain it. You can find strain tensors easily by using engineering strain like below.
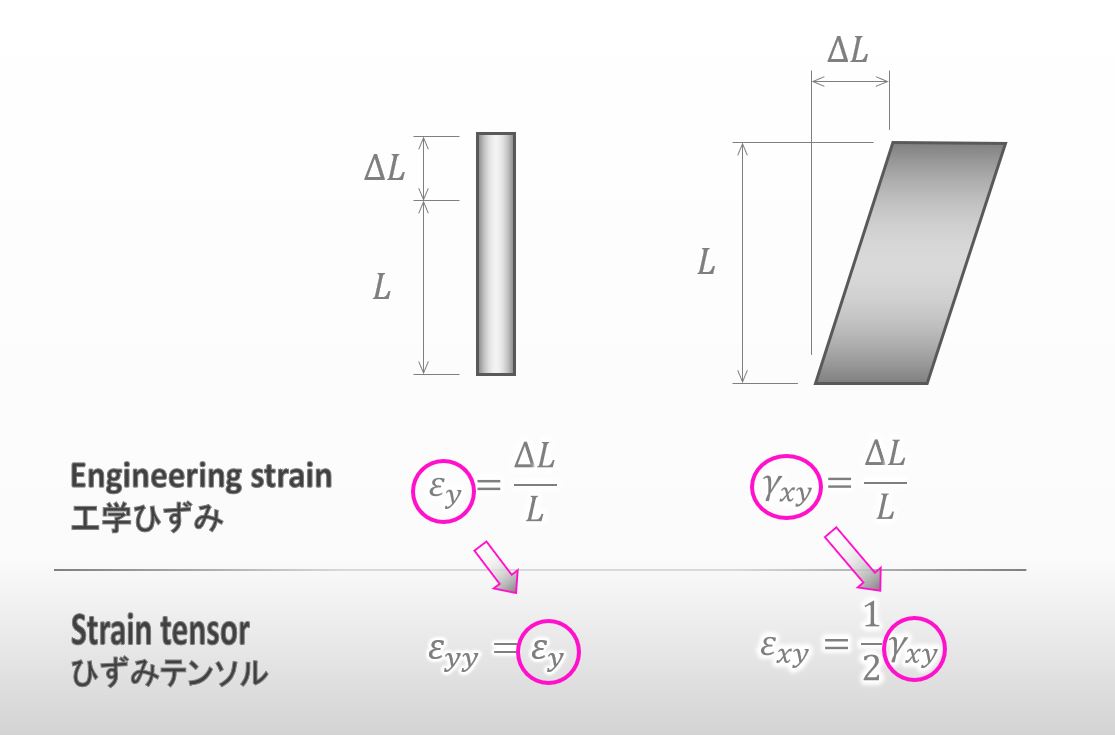
![]()
Let me give you a question. Let’ say you applied a force to a material and a point in the material moved a little to another point like below. Can you find the engineering strain at the point?
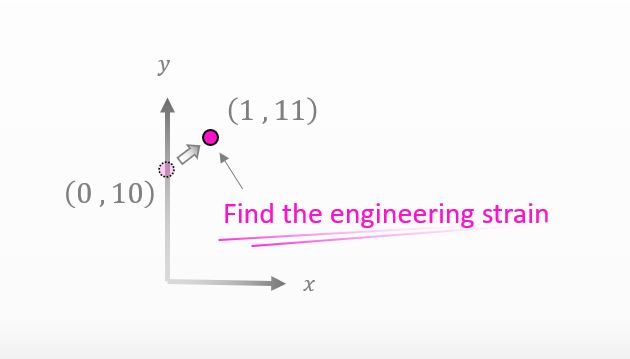
![]()
Well… It seems like a composition of normal strain and shear strain. Let me try to find the normal strain first. I feel like I can find it by using the expression of normal strain but…
![]()
Do you have a trouble?
![]()
Yeah.. Would you take a look at the figure below? When I use the expression of normal strain, I have to know both amounts of the stretch and the original length, right? I think I can calculate the amount of stretch. However, I have no idea to find the original length…

![]()
It may be necessary to define an original length in order to find a strain. There are cases in which strains are different from each other even though the displacements are the same. The figure below may enable you to easily imagine it.

![]()
I see.
What is the necessary condition to find a strain?
![]()
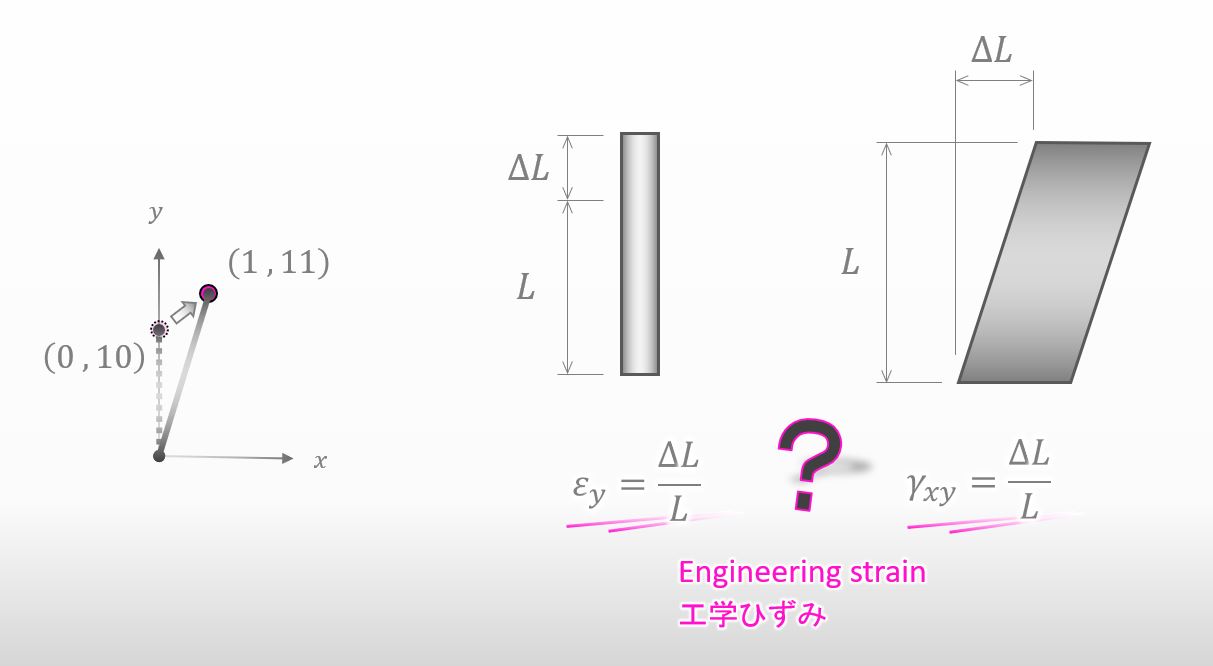
Then let’s say the original length in the material is the length between the origin and the point (0,10) like the figure below. Can you find the strain this time?
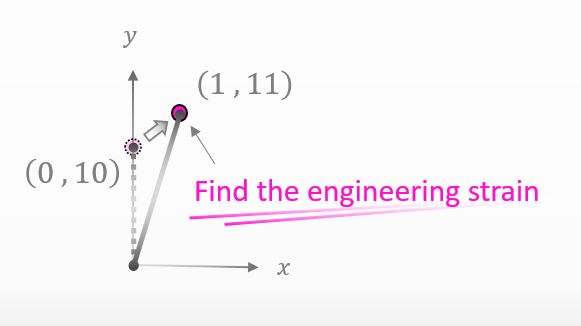
![]()
Well… I’d like to use the expressions below but I’m not sure how I can apply them to find the strain…
![]()
I feel like the expressions above are too simple to find the strain. I’m going to apply the authentic expressions of engineering strain shown below. By the way, “u” and “v” in the expression are displacements.

![]()
Do you think you can apply the expression to find the strain?
![]()
Well… I gave up, hahaha.
![]()
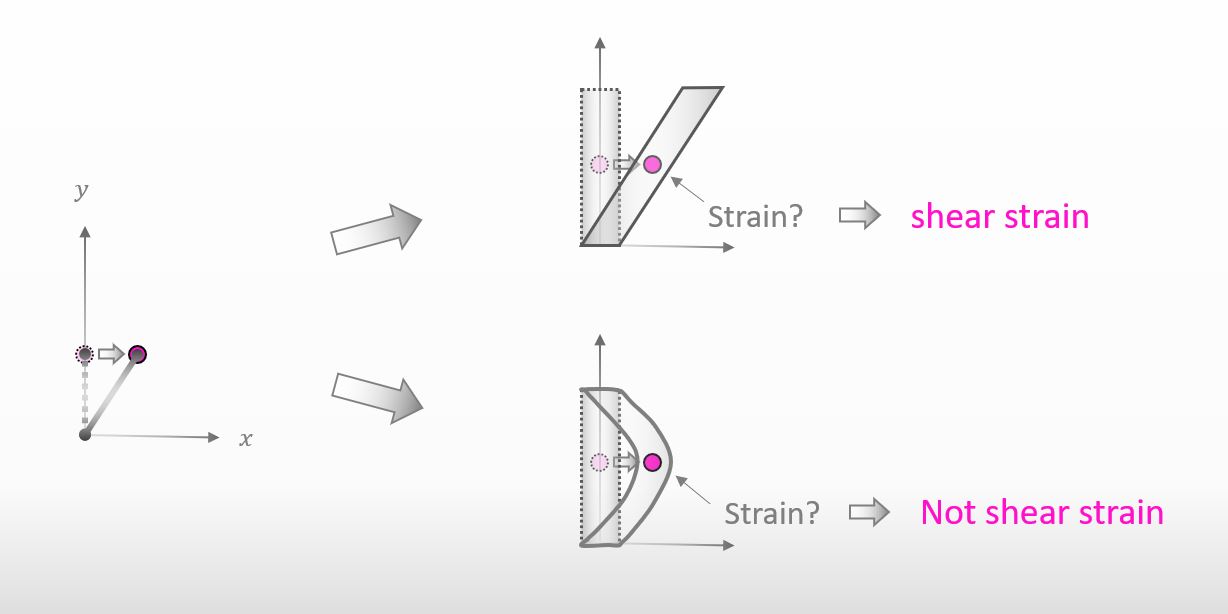
Please take a look at the figure below. The figure tells us that the strains are different from each other even though the displacements are the same.
![]()
Why can we say that the strain at the red point at the bottom in the figure is not shear strain?
![]()
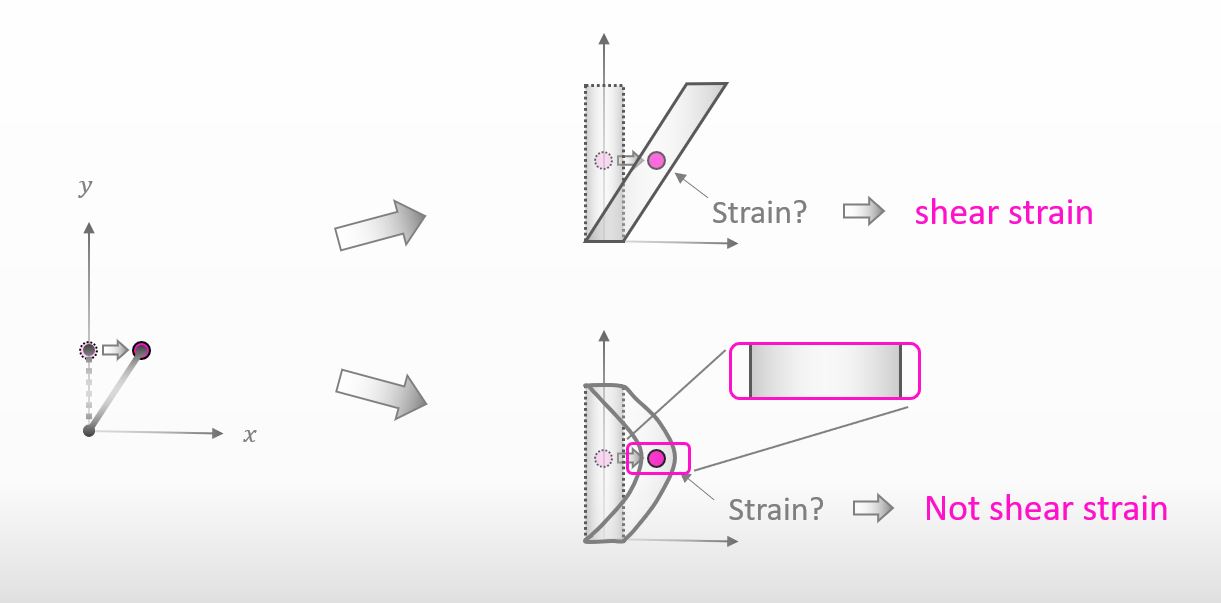
If you’d like to know the reason, you can enlarge the point like the figure below. The shape of the cylinder keeps its original shape. That’s why we can say that the shear strain is zero.
![]()
Right. The key point is that we can’t find the strain at a point even if we analyze how the point in a material moved.
![]()
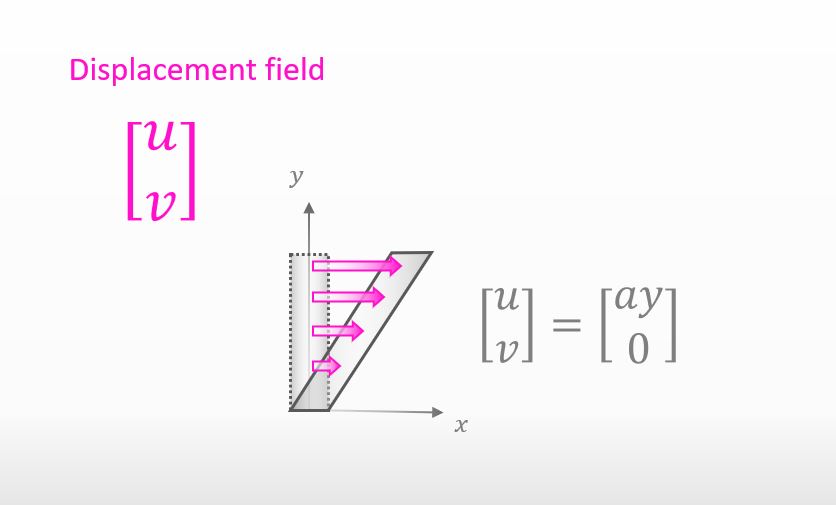
Exactly. In other words, we need to know the displacement field when we try to find a strain.
![]()
Can you give me an example of a displacement field?
![]()
I showed an example below.
![]()
Would you check the figure below? I tried finding the engineering strain.

![]()
Correct. Have you got along with strain?
![]()
For sure. Thank you.

