『ひずみ』ともっと親しもう

 

 

 

単純なひずみの例題、本当に解ける？

 

 

ペンギン先生。今日は材料力学の授業で ひずみ を学びました。

 

そうなんだ。で、どうだった？

 

とても簡単でした。材料を引っ張ってすこし伸びた場合、ひずみは下の図の様に計算されます。

 

 

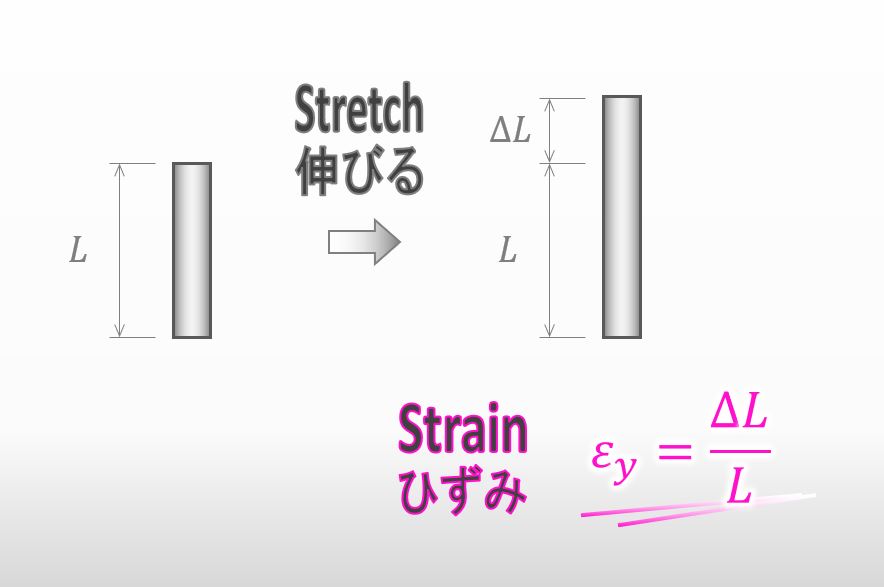
そうだね。

 

せん断ひずみ も習いました。材料がせん断方向に変形した場合、せん断ひずみは下の図の様に計算されます。

 

 

他に何か知ってることある？

 

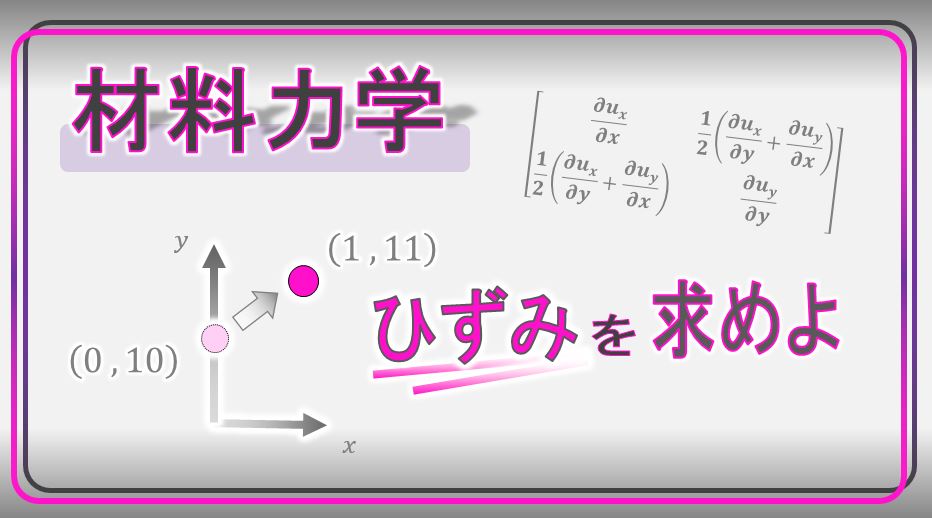
これまで話してきた ひずみ は、『工学ひずみ』 と呼ばれております。ひずみ に関して他の表現方法があります。『ひずみテンソル』 ってやつなんですけど。

 

 

工学ひずみ と ひずみテンソル の関係を説明してもらえる？

 

もちろん。そんなん簡単です。下の図の様に、工学ひずみ を使って ひずみテンソル を簡単に求めることができます。

 

 

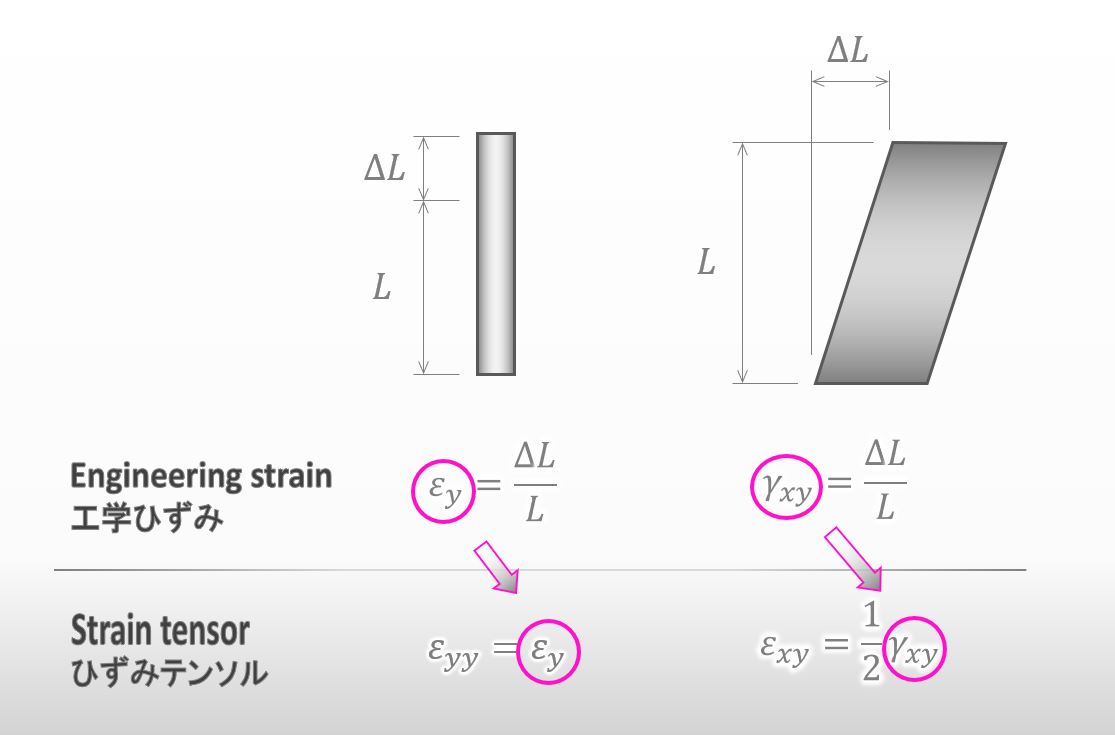
ひとつ質問なんだけど、下の図の様に ある材料に力を加えたらその物体内の点が少し移動したとしよう。この点の 工学ひずみ を求めることできる？

 

 

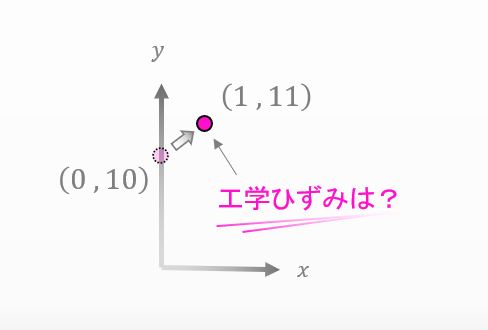
えぇっと… なんだか垂直ひずみとせん断ひずみの合成みたいな感じですね。まずは垂直ひずみから求めてみます。垂直ひずみの式を使えば求まると思うんですけど…

 

何か困ってる？

 

そうなんです… 下の図を見て頂けますか？　垂直ひずみの式を使うときには 伸びた量と元の長さを知らなければならないんですけど、伸びた量は計算できても 元の長さって何なのかわからないんです…

 

 

ひずみ を求める為には、元の長さを定義しておかなければならないのかもよ。下の図を見ればわかると思うけど、変位が同じでも ひずみ が異なってくる場合もあるしさ。

 

 

なるほど。

 

 

What is the necessary condition to find a strain?　ひずみ を求める為に必要な条件とは？

 

したら、下の図みたいに原点から(0,10)までの長さが材料内部の元の長さだったとしよう。これで ひずみ は求まるかな？

 

 

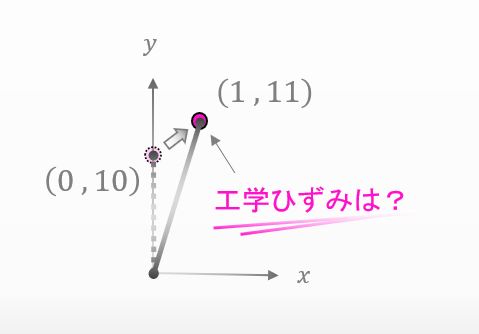
えぇっと… 下に示した式を使いたいんですけど、どう使って ひずみ を求めればよいのか…

 

 

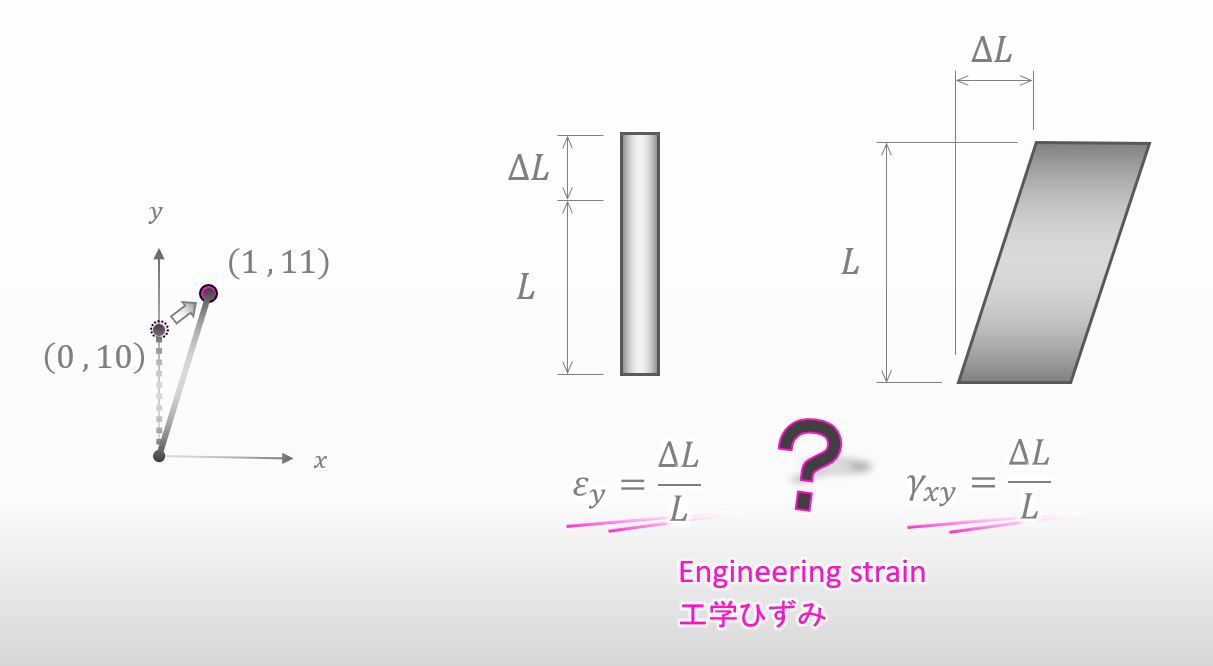
上の図のひずみの式は単純すぎて、今回の ひずみ の計算には使えないんだと思います。下に示す、ちゃんとした工学ひずみの式を使おうと思います。ちなみに式の中の u と v は変位を意味してます。

 

 

今回の場合その式使えそう？

 

ん～… ダメです。あはは…

 

下の図を見てごらん。変位が同じであっても ひずみ が異なることがわかるでしょ？

 

 

なんで下側の図の赤い点のひずみはせん断ひずみではないと言えるんですか？

 

下の図みたいに その点を拡大すると理由がわかりやすいかも。その部分の形は円筒形を保っているでしょ？だから せん断ひずみは 0 って言えるよね。

 

 

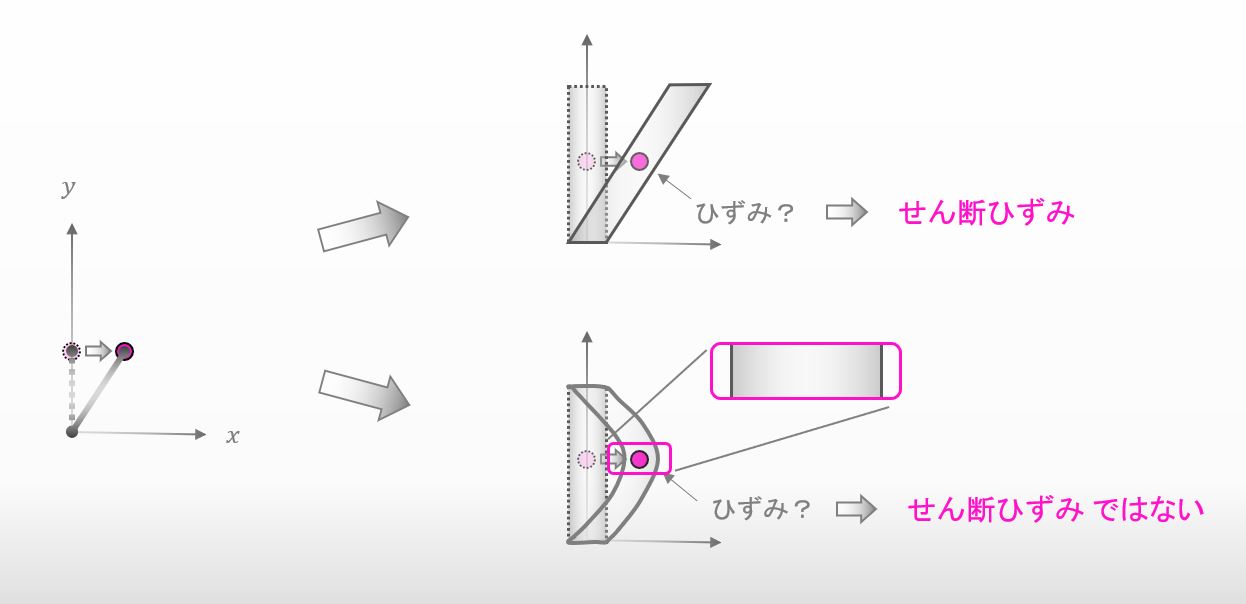
確かに。要は、ある点の移動だけ追っても その点のひずみを求めることは出来ないんですね。

 

そゆこと。ひずみ を求める為には、変位場がどうなっているのかを知る必要があるんだわ。

 

変位場の例ってどんなのがありますか？

 

下の例とかはどう？

 

 

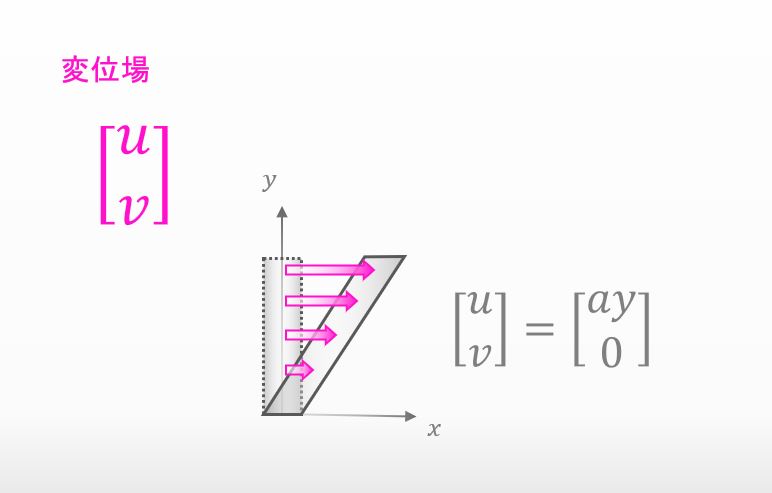
その変位場で工学ひずみを求めると、下の図の様に計算できますよね？

 

 

いいね。ひずみ とは仲良くなれた？

 

間違いなく。ありがとうございました。