What’s the difference between a tensor and a matrix?
Physical meaning of a tensor
Question about tensors
![]()
Hmm… What is a tensor..? What’s the difference between a tensor and a matrix..?
![]()
Did you call me?
![]()
Ah, Mr. Penguin. Nope.. I didn’t call you..
![]()
It seems like you are studying about tensors.
You are confusing a tensor with a matrix, aren’t you?
![]()
Actually… I am..
![]()
You don’t want to get the academic definition of a tensor but you’d like to get the image of a tensor, right?
![]()
Exactly!
![]()
If so, I think that we should think about the physical meaning of a tensor and that is the theme for today.
“What is the physical meaning of a tensor?”
First of all, let me ask you a question. Please give me an example of something that is NOT a tensor?
![]()
Well… I have no idea..
Characteristic of tensors (vectors)
![]()
That’s no problem. I’ll give you the example later.
I guess that you can give me an example of a tensor, can’t you?
![]()
According to a text book about tensors, a vector is one of tensors.
![]()
Good. Then, will you tell me the characters of a vector?
![]()
Well… A vector is a concept that has both a magnitude and a direction. Am I right?
![]()
Right. However, you are missing another important character of a vector.
The character is so obvious that it may be difficult to understand it. Please listen to what I’m going to say carefully.
A vector itself will not change even if the coordinate system changes into another one.
We can say the same thing to a tensor.
![]()
Well… Could you give me an example to help me understand it clearly?
![]()
Yes I can. As you know, a velocity is one of vectors.
There are two people in the picture below. Do you agree that the two people are looking at the same velocity vector?
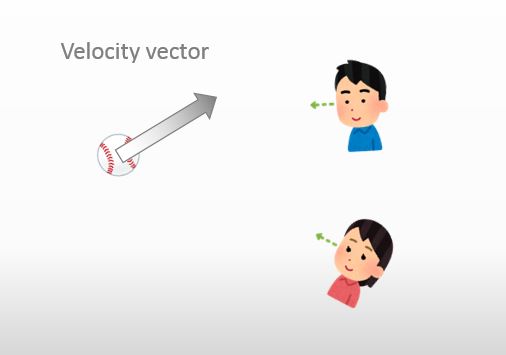
![]()
Well… I don’t know what you are saying well..
![]()
I’m just saying a very simple thing. Okay, let me change my question.
Do you think the situation in the picture below happens?
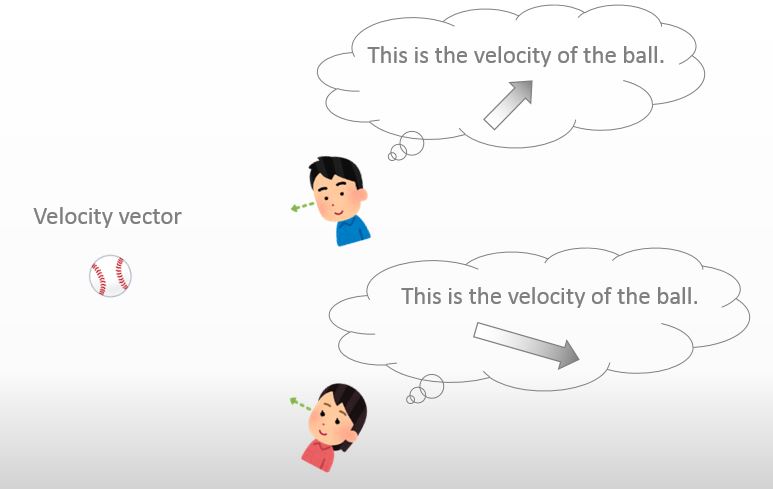
![]()
No. The situation will never happen.
The situation is like someone says that the ball goes east but another person says that the ball goes south with a different speed. If this happened, the world would be messy..
![]()
You are right. A vector doesn’t depend on who looks at. That is one of important characters of a vector.
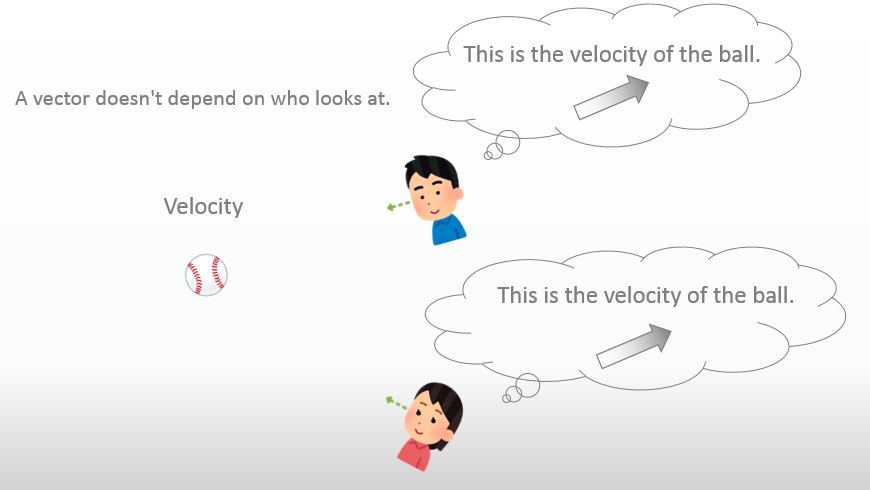
![]()
Hmm.. but if the coordinate system changes, the components of a vector will change accordingly. Am I wrong?
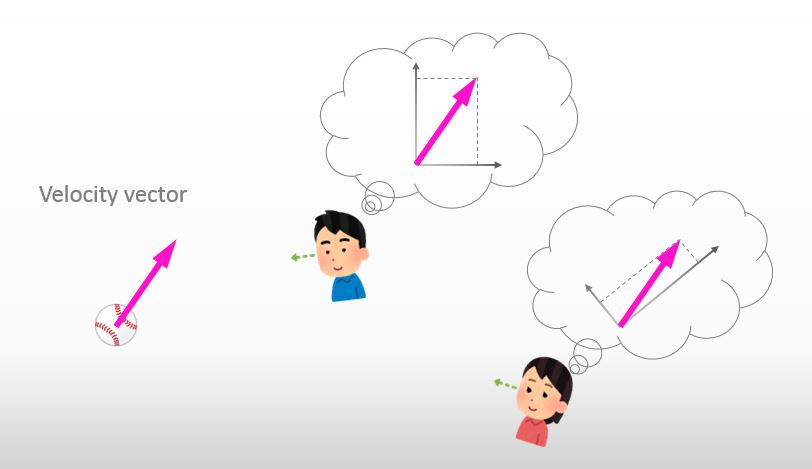
![]()
It is no doubt that the components of the vector changed. However, has the vector itself changed?
![]()
No… Both the magnitude and the direction of the vector have not changed at all.
![]()
Right. A vector itself will not change even if the coordinate system changes into another one.
We can say the same thing to a tensor. A tensor itself will not change even if the coordinate system changes into another one.
![]()
Okay but.. I am not sure if I get it right…
What is NOT a tensor?
![]()
Don’t be worried. I’ll guide you. I think you should know something that is NOT a vector.
I prepared a matrix below for you. The matrix expresses the numbers of dogs and cats that my neighbor Michael keeps.

![]()
It looks like a vector… but you said that you prepared something that is NOT a vector..
![]()
It can NOT be a vector. Let’s try to change the coordinate system into another one. Please take a look at the picture below.
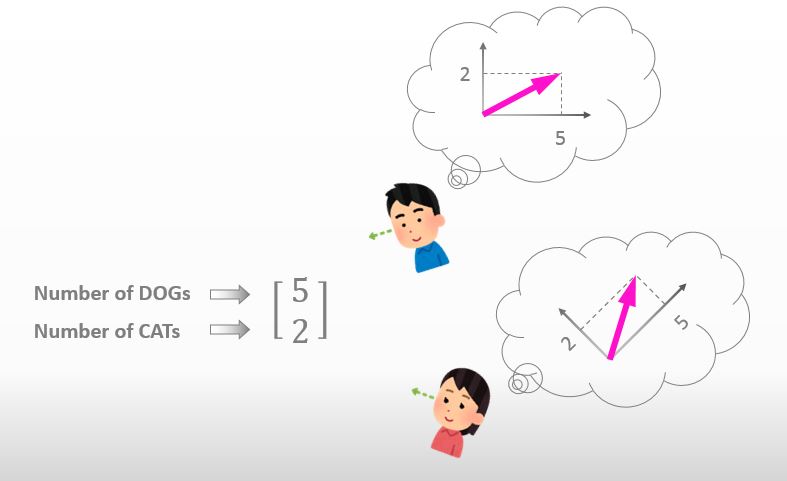
![]()
Wow.. the directions of the arrows are not the same…
![]()
Right. We can say that an arrow itself changes in response to a coordinate transformation and which means that the matrix above has a different concept of a vector and a tensor.
![]()
I feel like I understood the difference between a tensor and a matrix.
![]()
That’s good. Let’s call it a day.
