全微分とチェーンルール（連鎖律）に親しもう

 

 

 

 

 

 

 

全微分とチェーンルール（連鎖律）に関する疑問

 

本日は、２変数の全微分とチェーンルール（連鎖律）に親しもう というテーマでしゃべろうかと。

 

証明するのではなく、イメージをつかむってことですね。興味深いです。

 

全微分って聞いたことある？

 

学んだことがあります。２変数の全微分の式を下に示しました。x と y がわずかに変化したときの f(x) の変化量を意味してるらしいですけど。

 

 

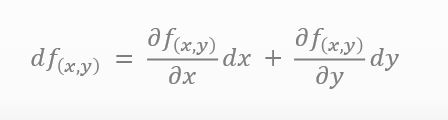
その理由は？

 

その授業では、下の図を先生に見せてもらって、この図が全微分を説明しているって教えてもらいました。

 

 

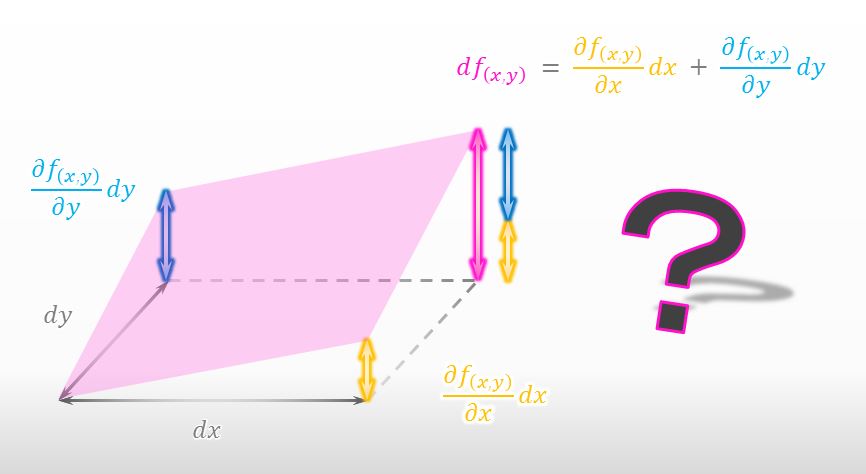
その説明で納得できた？

 

まぁ.. そんなもんなのかなと。

 

なるほど。じゃぁチェーンルール（連鎖律）ってのは学んだことある？

 

全微分を学んだあと、先生は全微分の式の両辺を下図の様に dt で割って、チェーンルールを導いていました。

 

 

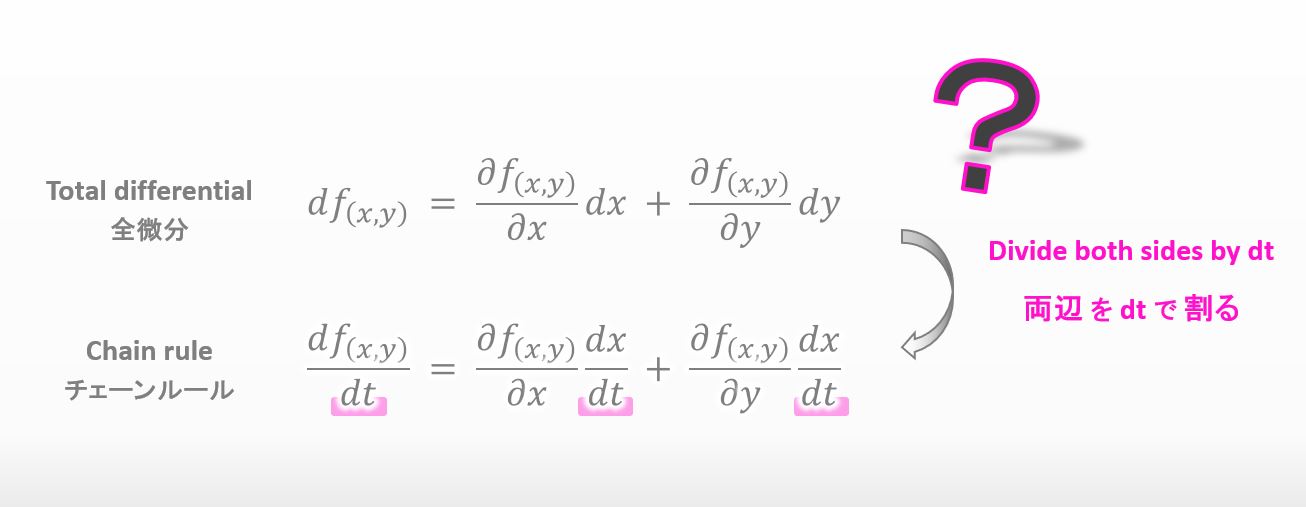
もしもパラメータt が時間なのだとしたら、チェーンルールは何を意味しているんだと思う？

 

えぇっと… わかりません…

 

したらチェーンルールの視覚的イメージができるように、この授業をすすめるよ。

 

どうも。授業が楽しみです。

 

まずは全微分から始めよう。

 

 

全微分のイメージをつかむ

 

今回の授業のために 3Dグラフを準備したから下を見てみて。

 

 

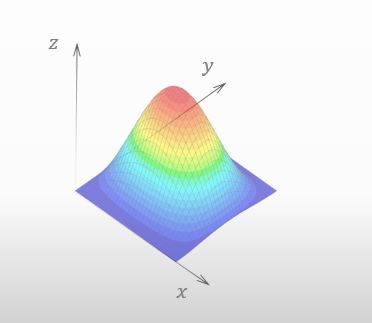
山みたいな形状ですね。

 

そうだね。で、下図の様に、山の小さな表面に注目してほしいんだけどさ。

 

 

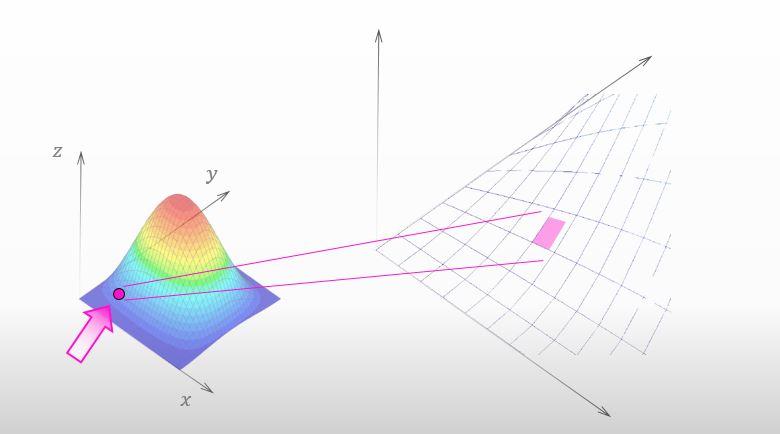
下の赤い四角形の高さが全微分だ ってことを、いつの日か授業で学びましたけど。

 

 

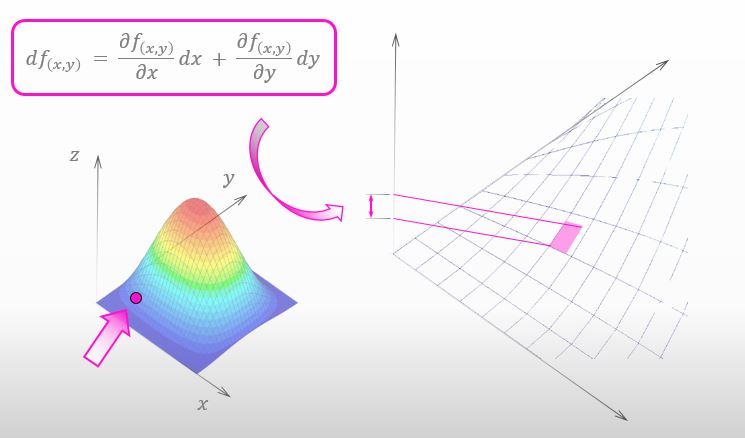
その四角形はどんな四角形？

 

たしか平行四辺形だったような…

 

これからその四角形を一緒にひとつずつチェックしていこう。

ってことで、今 山を歩いていて、下に示す点にいるとしよう。

 

 

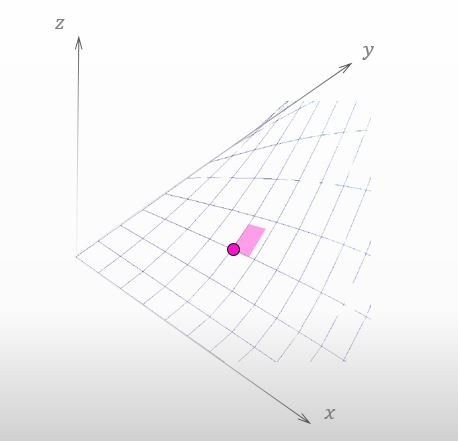
で、下の図の様に y の値を変えないで移動したとしよう。正確に言うと、x-y平面に投影された『影』が x軸方向に dx だけ移動したってことなんだけどさ。

 

 

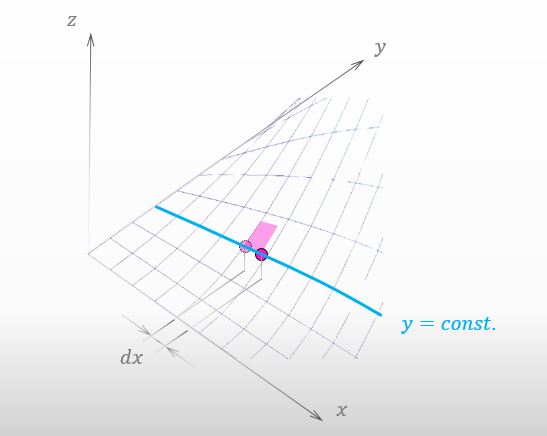
上の図の青い曲線は何ですか？

 

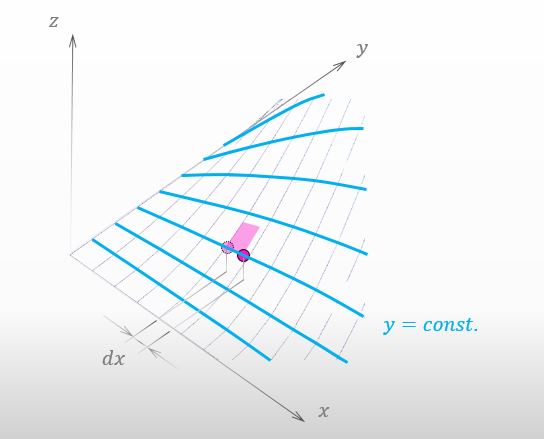
あ、言い忘れてた。下の図を見てみて。青い曲線上では y の値に変化はないのよ。

 

 

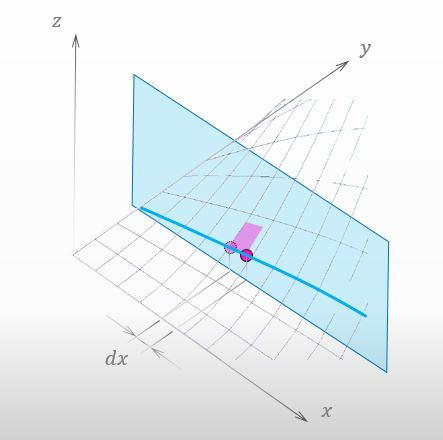
下の図みたいに y軸に垂直な平面を置いてみると、青い曲線上では y の値は変化しない ってことを簡単にイメージできますよね。山と平面との交線が青い曲線ってことになるんですけど。

 

 

良い図を描いてくれたね。dx が青い曲線の長さではなくて、x軸方向に移動した影の長さだ ってことが簡単にわかるわ。

 

質問なんですけど、青い曲線上を移動しながら 私はどれくらい山を登ったんですか？

 

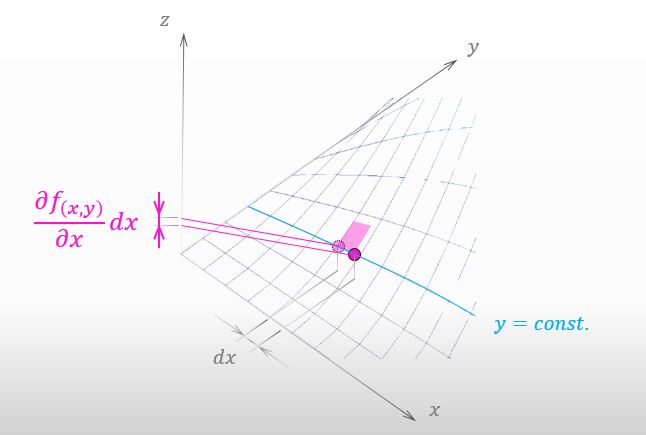
下の図を見てみて。山を登った量が示されてるからさ。

 

 

あ、それは以前にペンギン先生の授業で学びました。その授業は２次元の話でしたけど。微小変化と近似に親しもう という授業でしたね。

 

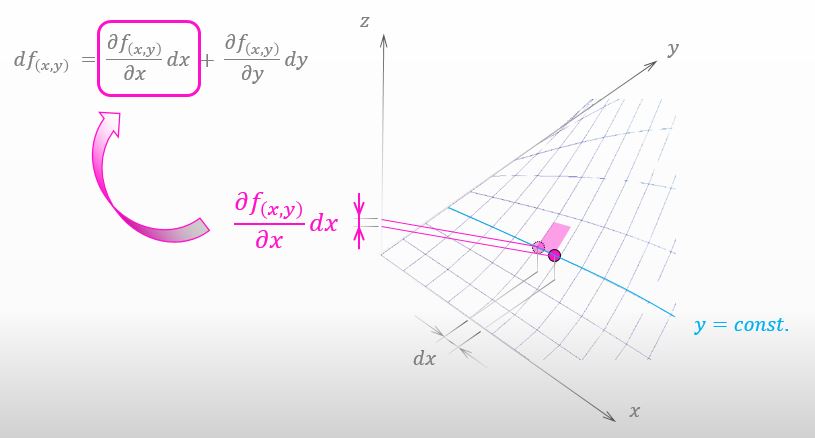
どうも。覚えていてくれたのね。今回山を登った量は、全微分の式においては下図の様に左側の項になるわけよ。

 

 

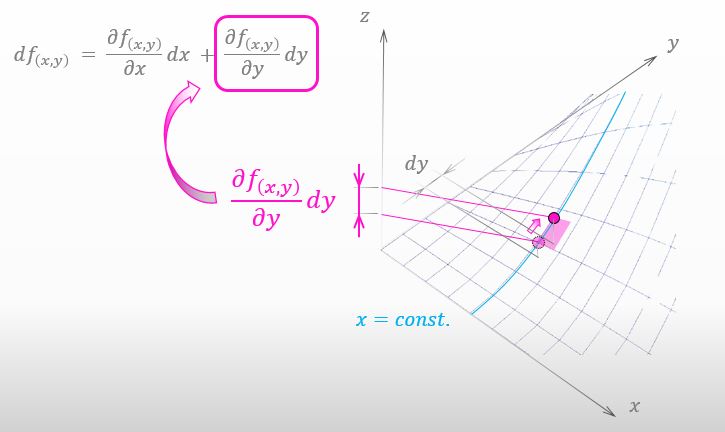
影が x軸方向に動いたらどうなるのかは理解できました。y軸方向でも同様のことが起きますよね。つまり、もし影が y軸方向に dy だけ動いたのなら、下の図の様に 山を登った量は全微分の右側の項となる ってことなんですけど。

 

 

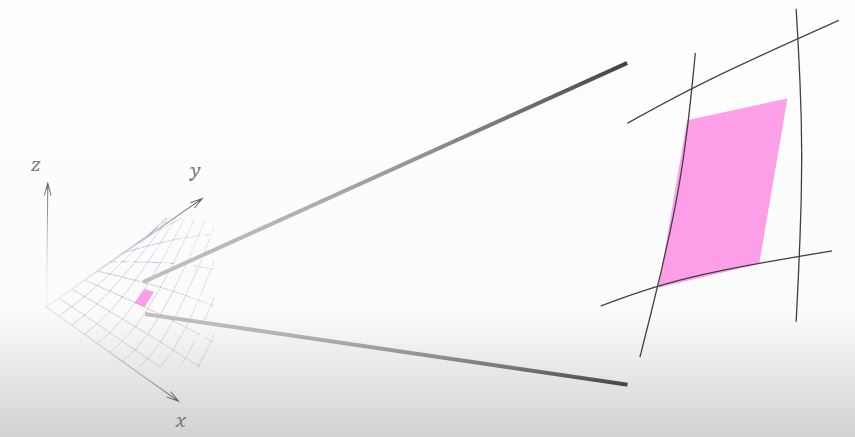
そうだね。実は今、全微分の意味を理解する準備が整ったんだわ。今まで考えてきた小さな赤い面を拡大したから 下の図を見てみて。

 

 

確かその赤い面の形状は、平行四辺形でしたよね。

 

そうだね。この平行四辺形は、下図の様に３つの点から成り立ってんだわ。

 

 

平行四辺形は３点が決まれば形状が決まりますもんね。

 

その平行四辺形において、今わかっていることを教えてくれる？

 

先程 私が登った高さですね。下に示しました。

 

 

ありがとう。で、何か気付くことある？

 

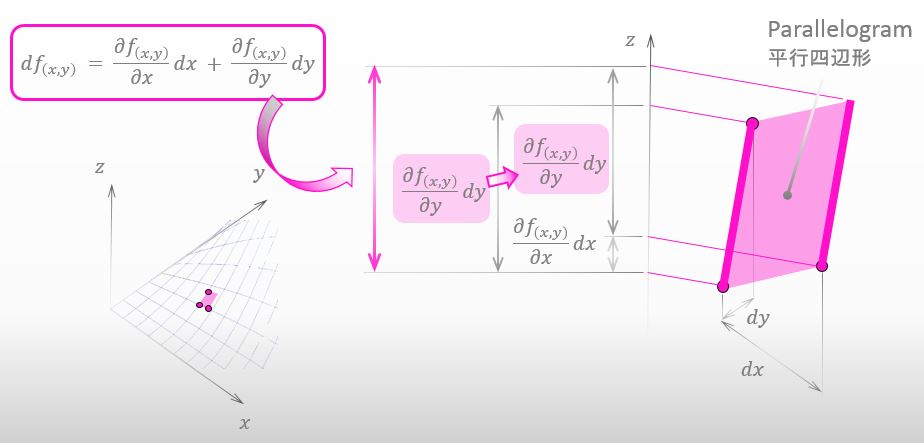
私たちが考えている形状は平行四辺形なので、下に示す様に、平行四辺形の全体の高さは全微分の値と等しくなります。

 

 

いいじゃん。これで全微分のイメージはつかめたね。

 

 

全微分を理解する為のキーポイント

 

全微分のキーポイントは、dx と dy は互いに独立しているってことなんだわ。

 

どゆこと？

 

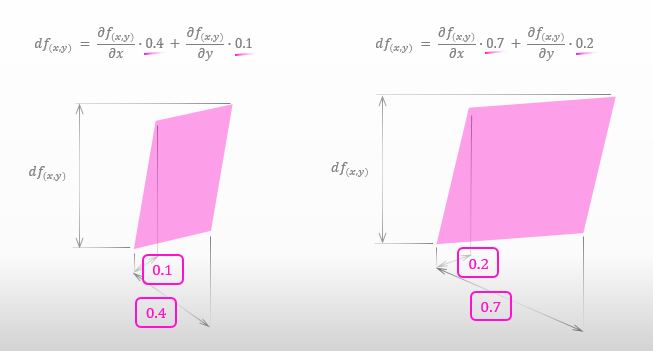
例えば、下図の両方の状況共に 全微分の考え方を使うことができる ってこと。dx と dy は共に好き勝手な値をとれるからさ。ただし注意してもらいたいことは、平行四辺形が小さければ小さいほど、全微分の近似は正確になる ってこと。

 

 

なんで dx と dy が独立している ってことが全微分のキーポイントなんですか？

 

なんでかって言うと、チェーンルールでは異なってくるからね。

 

 

チェーンルール（連鎖率）を視覚的に理解する

 

全微分とチェーンルール（連鎖率）を比較してみてくれる？

 

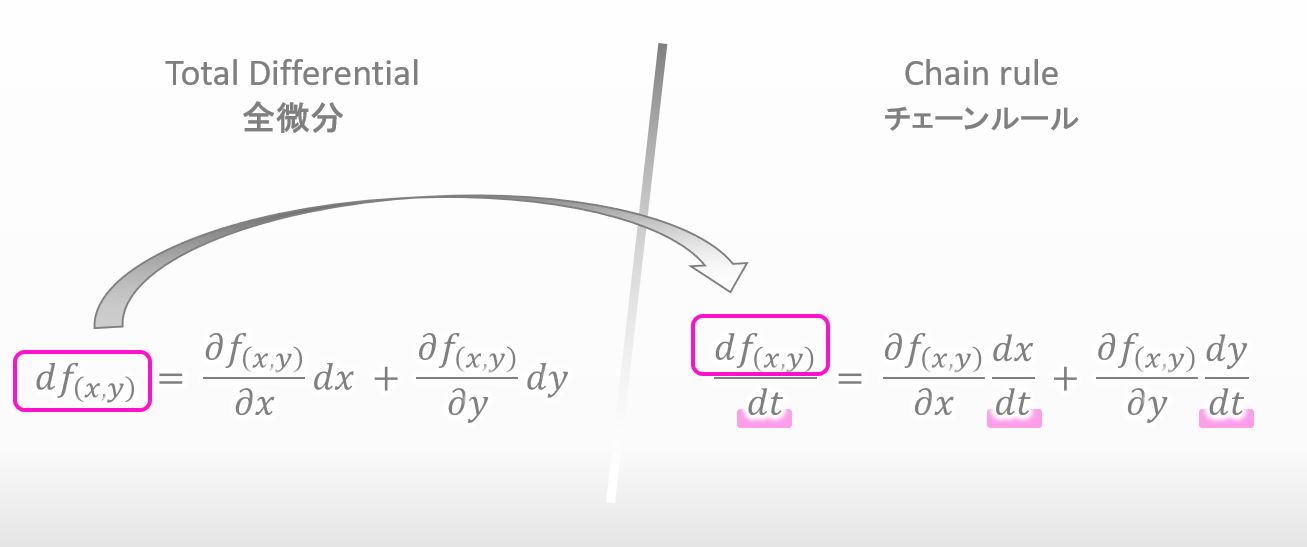
下を見てみて下さい。チェーンルールの式には全微分が含まれてますね。式の形的には、全微分の両辺を dt で割っているのがチェーンルールのイメージです。

 

 

そう見えるね。２変数の全微分の意味はまだ覚えてる？

 

x-y平面に投影された影が少し移動したとき、どれくらい山を登ったか ってことですよね。

 

 

チェーンルールの式の形的には、山を登った量を dt で割っている様に見えるわけだ。

 

 

登った量の『t』に対する変化率を表しているわけですね？

 

パラメータt の意味を視覚的に理解するには、チェーンルールにおいて dx と dy が関係しあっているってことを理解しておかなきゃならないんだわ。

 

dx と dy はどう関係しあっているんですか？

 

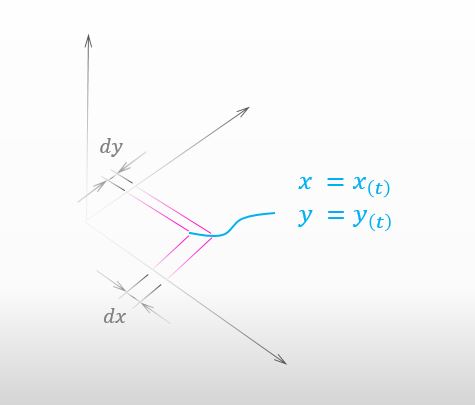
下の図の様に、x-y平面上の曲線をイメージするといいかもね。

 

 

なるほど。dx と dy は好き勝手に値を取れないですね。曲線上に拘束されているので。

 

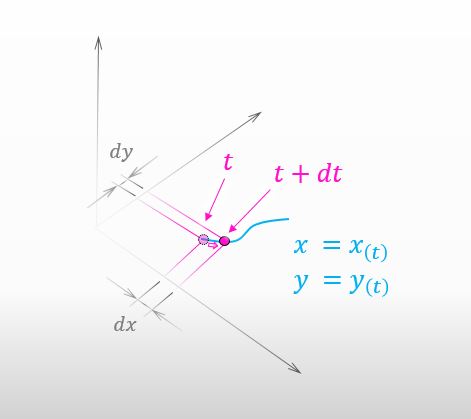
そゆこと。下の図の様に、少しだけ t の値が変化したしよう。

 

 

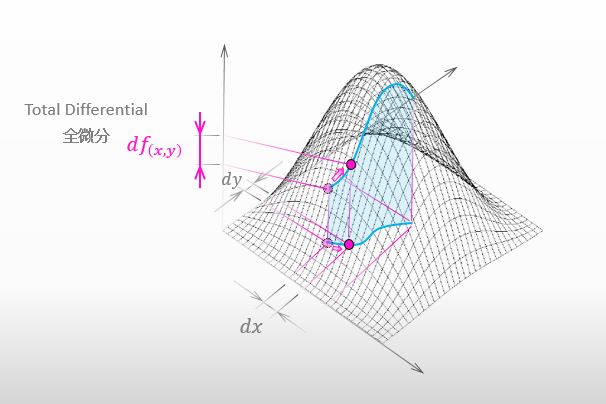
私の影が青い曲線上を少し動いた ってことですね。このとき、私が山を登った量は下図の様に表すことができますね。

 

 

おっしゃる通り。もしもパラメータ t が時間なのだとしたら、チェーンルールは何を意味しているんだと思う？

 

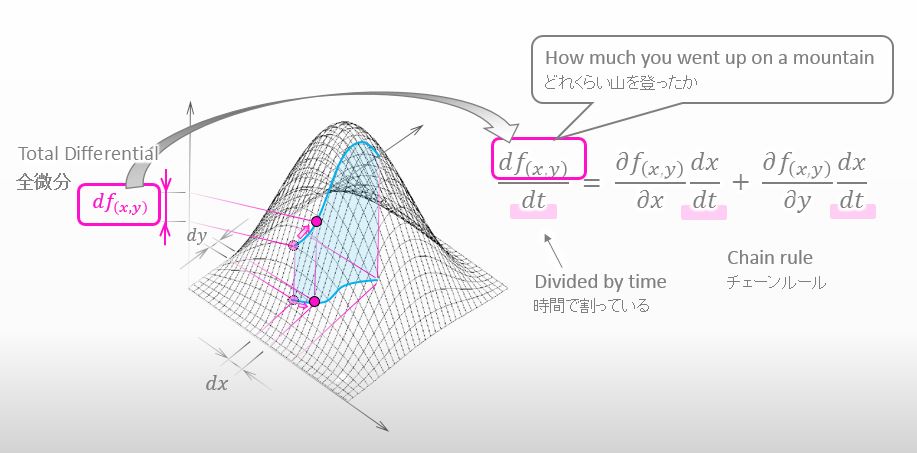
もし t が時間だとすると、チェーンルールは登った量を時間で割ることになりますね。ってことは、チェーンルールが示していることは、単位時間当たりにどれくらい山を登るのか ってことになります。

 

 

完璧だね。チェーンルールの視覚的イメージはついた？

 

はい。どうもありがとうございました。